Изображения синусоидальных функций времени в векторной форме

При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими. Для упрощения расчетов пользуются либо векторным представлением тригонометрических функций, либо комплексным представлением.

Задача упрощается, если представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию 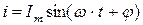. Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.

Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси " 0 ", ось направлена на нас из толчки “ 0 ”, из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени . Когда отрезок повернется на угол α₁, проекция его 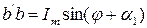. Откладывая углы α₁, α₂,... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 3.1).

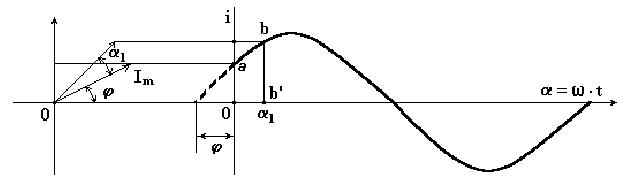
Рисунок 3.1. Вектор на координатной плоскости, соответствующий синусоидальной зависимости тока i с амплитудой I_m от времени t с частотой ω и начальной фазой φ.

Представим синусоидальные токи i₁ и i₂ в виде двух радиус - векторов, длина которых равна в соответствующем масштабе амплитудам соответствующих переменных токов I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ₁ и φ₂ относительно горизонтальной оси. Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 3.2).Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.

Рисунок 3.2. Сложение в векторной форме синусоидальных токов с амплитудами I_1m и I_2m и начальными фазами φ₁ и φ₂ и результирующий ток I_3m с начальной фазой ψ₃. Все три тока колеблются с одной и той же частотой ω.

Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины. Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью, длины этих векторов равны амплитудам соответствующих величин (тока, напряжения, ЭДС). Положительным считается направление вращения векторов против часовой стрелки.

Дата добавления: 2014-01-06