Изображение синусоидальных функций времени в комплексной форме

При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам.

Из курса математики известно, что комплексное число C может быть записано в показательной или алгебраической форме:

(3.4)

где с - модуль комплексного числа, φ - аргумент, a - вещественная часть комплексного числа (обозначается Re (C)), b - мнимая часть (обозначается Im(C)), j - мнимая единица, j = .

(3.5)

С помощью формулы Эйлера можно перейти от показательной формы записи к алгебраической.

(3.6)

От алгебраической формы записи переходят к показательной форме с помощью формул (3.5).

Комплексное число может быть представлено в виде радиус - вектора в комплексной плоскости. Вектор длиной, равной модулю С, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.3.3).

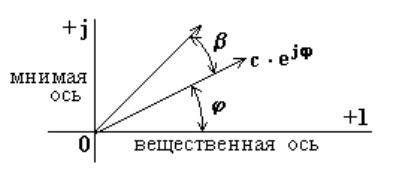
Рисунок 3.3. Представление мнимых чисел на комплексной плоскости.

Умножим комплексное число 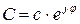на множитель 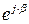. Радиус - вектор на комплексной плоскости повернется на угол β. Множитель β называется поворотным. Новое комплексное число (новый вектор) будет иметь вид: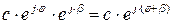

Если 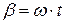, то вектор, умноженный на 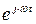, превратится во вращающийся с угловой скоростью w радиус вектор, аналогично тому, как мы представляли на векторной диаграмме.

Таким образом, например, косинусоидальное напряжение

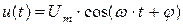(3.7)

мы можем представить, по аналогии с векторными диаграммами в виде вращающегося на комплексной плоскости вектора вида: 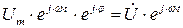, величина называется комплексной амплитудой напряжения (начальное, при t=0 положение вектора, соответствующему u(t) на комплексной плоскости). Комплексные амплитуды тока и ЭДС вводятся аналогичным образом.

Рассмотрим вещественную часть полученного нами вектора на комплексной плоскости:

(3.8)

Вещественная часть произведения комплексной амплитуду напряжения на множитель 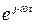совпадает с формулой для косинусоидального вещественного напряжения (3.7). Если бы мы задали напряжение в синусоидальной форме 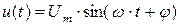, то, для получения исходного напряжения из комплексного вектора, мы должны в выражении (3.8) рассматривать мнимую часть ()

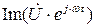Законы Ома и Кирхгофа в комплексной форме:

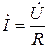- закон Ома

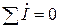- первый закон Кирхгофа

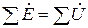- второй закон Кирхгофа

Дата добавления: 2014-01-06