Метод узловых потенциалов

Метод расчета электрических цепей, в котором за неизвестные принимаются потенциалы узлов, называется методом узловых потенциалов. Допустим, в схеме у узлов. Так как любая одна точка схемы может быть заземлена без изменения токораспределения в схеме, то один из узлов можно заземлить, т.е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с у до (у – 1).

Число неизвестных в методе узловых потенциалов равно числу уравнений, которые нужно составить для схемы по первому закону Кирхгофа. В тех случаях, когда (у – 1) меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.

Обратимся к схеме рис. 1.28.

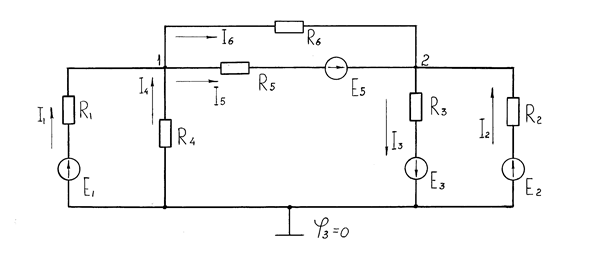
Рис. 1.28. Схема четырехконтурной электрической цепи с четырьмя источниками э.д.с.

Принимаем потенциал одного из узлов схемы, например, третьего, равным нулю, обозначим положительные направления токов и записываем уравнения по первому закону Кирхгофа для первого и второго узлов:

I ₆ + I ₅ – I ₁– I ₄ = 0;

I ₃ – I ₂ – I ₆ – I ₅ = 0.

Токи в ветвях схемы:

I ₆ = (φ ₁– φ ₂) g ₆; I ₅ = (φ ₁– φ ₂ + Е ₅) g₅ ;

I ₂ = (– φ ₂ + Е ₂) g ₂; I ₃ = (φ ₂ + Е ₃) g ₃;

I ₁ = (– φ ₁ + Е ₁) g ₁; I ₄ = (– φ ₁ ) g ₄ .

Подставим значения токов в уравнения, составленные по первому закону Кирхгофа:

φ ₁ g ₆ – φ ₂ g ₆ + φ ₁ g ₅ – φ ₂ g ₅ + Е ₅ g ₅ + φ ₁ g ₁ – Е ₁ g ₁ + φ ₁ g ₄ = 0

φ ₁ g ₃ + E ₃ g ₃ + φ ₂ g ₂ – E ₂ g ₂ – φ ₁ g ₆ + φ ₂ g ₆ – φ ₁ g ₅ + φ ₂ g ₅ – E ₅ g ₅ = 0.

Производим группировку членов:

φ ₁ (g ₆ + g ₅ + g ₁ + g ₄) – φ ₂ (g ₆ + g ₅) = Е ₁ g ₁ – Е ₅ g ₅

– φ ₁ (g ₆ + g ₅) + φ ₂ (g ₃ + g ₂ + g ₆ + g ₅) = Е ₂ g ₂ – Е ₃ g ₃ + Е ₅ g ₅ ,

где: g ₆ + g ₅ + g ₁ + g ₄ = g ₁₁ – собственная проводимость первого узла;

g ₃ + g ₂ + g ₆ + g ₅ = g ₂₂ – собственная проводимость второго узла;

g ₆ + g ₅ = g ₁₂ = g ₂₁ – общая узловая проводимость.

Окончательно получаем:

φ ₁ g ₁₁ – φ ₂ g ₁₂ =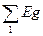

– φ ₁ g ₂₁ + φ ₂ g ₂₂ = .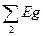

В результате решения системы уравнений известными методами определяем φ ₁ и φ ₂.

Подставляя значения φ ₁ и φ ₂ в уравнения для токов, находим действительные токи в ветвях схемы.

Дата добавления: 2014-01-06