Цілі й дробові (як додатні, так і від’ємні) числа утворюють множину раціональних чисел, яку позначають буквою

Наприклад, .

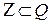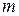Зрозуміло, що . Кожне раціональне число можна подати у вигляді відношення , де - ціле число, а 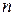- натуральне.Наприклад, .

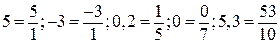З можливістю такого подання пов’язана назва «раціональне число»: одним з перекладів латинського слова ratio є «відношення».

Кожне раціональне число можна подати у вигляді скінченного десяткового дробу або у вигляді нескінченного періодичного десяткового дробу. Для дробу таке подання можна отримати, виконавши ділення числа 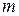на число 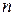«куточком». Наприклад, .

Число 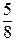записано у вигляді скінченного десяткового дробу, а число - у вигляді нескінченного періодичного десяткового дробу. У запису 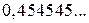цифри 4 і 5 періодично повторюються. Групу цифр, яка повторюється, називають періодом дробу і записують , тобто .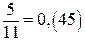

Зауважимо, що будь-який скінченний десятковий дріб і будь-яке ціле число можна подати у вигляді нескінченного періодичного десяткового дробу. Наприклад,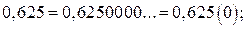

.

Отже, кожне раціональне число можна подати у вигляді нескінченного десяткового періодичного дробу.

Справедливим є й таке твердження: кожний нескінченний десятковий періодичний дріб є записом деякого раціонального числа.

Сума, різниця, добуток і частка (крім ділення на нуль) двох раціональних чисел є раціональними числами.

4. Виникае природне запитання: існують числа які не є раціональними? Відповідь: існують. Наприклад: ; . Ці числа не є раціональними. Їх називають ірраціональними (приставка «ір» означає заперечення).

Ірраціональні числа можуть бути подані у вигляді нескінченних неперіодичних десяткових дробів.

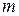Жодне ірраціональне число не можна подати у вигляді дробу , де - ціле число, а 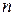- натуральне, а отже, й у вигляді нескінченного періодичного десяткового дробу.

5. Множини ірраціональних і раціональних чисел утворюють множину дійсних чисел, яку позначають буквою .

Тепер «ланцюжок» можна продовжити:.

Над дійсними числами можна виконувати чотири арифметичних дії (крім ділення на нуль), у результаті отримуватимемо дійсне число. Цим діям притаманні звичні для вас властивості:

переставна властивість додавання

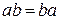переставна властивість множення

сполучна властивість додавання

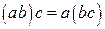сполучна властивість множення

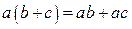розподільна властивість

Додатні дійсні числа можна порівнювати, використовуючи правила порівнювання десяткових дробів, тобто порівнювання цифр у відповідних розрядах. Наприклад, .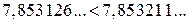

Будь-яке додатне дійсне число більше за нуль і за будь-яке від’ємне дійсне число. Будь-яке від’ємне дійсне число менше нуля.

Знаходячи довжину кола і площу круга, ви користувалися наближеним значенням числа . Аналогічно при розв’язуванні практичних задач, де необхідно виконати дії з дійсними числами, ці числа замінюють їх наближеними значеннями. Наприклад, .

Дата добавления: 2014-01-06