Представление дробных чисел

Дополнительный код.

Вопросы

1.Перевод дробных чисел из десятичной системы счисления в систему счисления с основанием q.

2. Перевод дробных чисел из десятичной системы счисления в систему 2-ю и 8-ю системы счисления.

4. Перевод дробных чисел из десятичной системы счисления в 16-ю систему счисления.

5. Перевести число 0.35 в 2- системы счисления.

6. Перевести число 0.35 в 8-ю систему счисления.

7. Перевести число 0.35 в 16-ю систему счисления.

8. Хранение в ЭВМ целых чисел 15, 234, 127, 34 (в 2-х байтах).

9. Двоичное число без знака.

10. Обратный код числа

11. Представить в обратном коде 19, 125, -15, -127, -57.

Лекция № 6

Для образования дополнительного кода коэффициент С выбирают равным C = 2ⁿ.

Тогда значение числа определяется выражением:

,

где d_n, d_{n -1},..., d ₁, d ₀ - цифры и соответствующие веса цифр: 0 и 1; d_n - дополнительный знаковый разряд, для неотрицательных чисел равен 0 (d_n = 0), для отрицательных чисел равен единице (d_n = 1); d_nd_{n -1}... d ₁ d ₀ - запись целого (n +1)-разрядного отрицательного числа в дополнительном коде; n, п - 1,..., 1, 0 - номера разрядов; d_i ´ 2 ⁱ - весовой коэффициент i -го разряда дополнительного кода числа (i = 0, n -1). Весовой коэффициент n -го разряда дополнительного кода числа равен 2 ⁿ.

Пусть в дополнительном коде число имеет вид: 1100. Тогда это число в прямом коде равно:

N = 1 ´ (-2³) + 1 ´ 2² + 0 ´ 2¹ + 0 ´ 2⁰ = -8 + 4 + 0 + 0 = -4₁₀ = -100₂.

Пусть в дополнительном коде число имеет вид: 0100. Тогда это число в прямом коде равно:

N = 0 ´ (-2³) + 1 ´ 2² + 0 ´ 2¹ + 0 ´ 2⁰ = 0 + 4 + 0 + 0 = 4₁₀ =+100₂.

Найдем правило записи отрицательного числа в прямом коде, представленном в дополнительном коде:

;

;

.

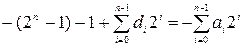Так как 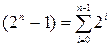,то:

;

;

;

.

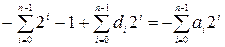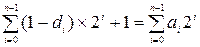Чтобы записать прямой код отрицательного числа, представленного в n -разрядном дополнительном коде, необходимо:

1) отбросить знаковый разряд d_n;

2) найти обратный код полученного числа. Для этого необходимо заменить в разрядах d_i (i =0, n -1) нули единицами, а единицы - нулями;

3) к полученному числу прибавить единицу. При этом будет получена абсолютная величина искомого отрицательного числа в двоичной системе счисления;

4) слева приписать к полученной абсолютной величине знак «минус».

Пример 6. Найдем запись двоичного числа в прямом коде, если его четырехразрядный дополнительный код равен 1100.

1. Отбросим старший разряд: 1100 ® 100.

2. Найдем обратный код дополнительного кода числа:

100

3. К полученному числу прибавим единицу:

011₂ + 1₂ = 100₂.

4. Слева к полученному числу припишем знак «минус»:

100₂ ® -100₂.

Пример 6.2. Найдем запись двоичного числа в прямом коде, если его четырехразрядный дополнительный код равен 1000.

1. Отбросим старший разряд: 1000 ® 000.

2. Найдем обратный код дополнительного кода числа:

000

3. К полученному числу прибавим единицу:

111₂ + 1₂ = 1000₂.

4. Слева к полученному числу припишем знак «минус»:

1000₂ ® -1000₂.

Пример 6.3. Найдем запись двоичного числа в прямом коде, если его четырехразрядный дополнительный код равен 1111.

1. Отбросим старший разряд: 1111 ® 111.

2. Найдем обратный код полученного числа:

111

3. К полученному числу прибавим единицу:

0₂ + 1₂ = 1₂.

4. Припишем знак «минус»:

1₂ ® -1₂.

Определим правило нахождения n разрядного дополнительного кода целого m- разрядного отрицательного числа:

;

;

;

.

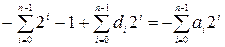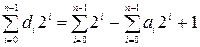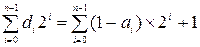Чтобы найти представление m- разрядного двоичного целого отрицательного числа в дополнительном коде с количеством двоичных разрядов n (n > m) необходимо выполнить следующие действия:

1) дополнить число слева n-m нулями до разрядности n, a_n = 0;

2) найти обратный код полученного числа. При этом двоичные нули исходного числа заменяются двоичными единицами, а двоичные единицы - двоичными нулями, 1 - a_n становится равным единице;

3) к полученному обратному коду прибавить единицу.

Пример 6.4. Найдем шестиразрядный дополнительный код числа -100₂.

1. Дополним исходное число до необходимой разрядности:

100 ® 00100.

2. Найдем обратный код полученного числа:

00100

3. Прибавим единицу к полученному коду:

11001 + 1 =11010.

4. Припишем единицу знакового разряда:

11010 ® 111010.

Заметим, что отрицательные целые n -разрядные числа вида -2 ^{n -1} можно записать в дополнительном коде с n разрядами.

Пример 6.5. Найдем шестиразрядный дополнительный код шестиразрядного числа -2⁵.

1. Дополнять исходное число -2^{5 =} -100000₂ до разрядности равной 6 в этом случае нет необходимости. Число -2⁵ уже шестиразрядное.

2. Найдем значения 1 - a _i (i = 1, 6):

a_i 100000

1 - a _i 011111

3. Прибавим единицу к полученному числу:

011111 + 1 =100000.

4. Припишем единицу знакового разряда слева к числу в этом случае нет необходимости, так как уже b ₅ = 1.

Таким образом, дополнительный код числа -2⁵ равен 100000. Проверим результат преобразования.

1. Отбросим знаковый разряд:

00000.

2. Восстановим прямой код полученного числа:

11111.

3. К полученному числу прибавим единицу:

11111₂ + 1₂ = 100000₂.

4. Слева к полученному числу припишем знак «минус»:

100000₂ ® -100000₂.

Полученный результат совпал с исходным числом:

-100000₂ = -2⁵.

Значения минимальных отрицательных и максимальных положительных целых чисел, которые можно хранить в дополнительном коде в словах размера 1, 2, 4 и 8 байтов, показаны в табл. 6.1. При заполнении таблицы использовались выражения для определения минимального отрицательного и максимального положительного числа:

L _min = -2^{8´ l –1}; (6.1)

L _max = 2^{8´ l –1} - 1, (6.2)

где L _min - минимальное целое отрицательное число, представленное в обратном коде; L_max - максимальное целое положительное число, представленное в обратном коде; l - размер слова в байтах.

Таблица 6.1

Размер слова в байтах	Размер слова в битах	Значение минимального числа	Значение максимального числа
		-2^7= -128	(2^7 -1)= 127
		-2^15 = -32768	(2^15 - 1) = 32767
		-2^31 = -2147483648	(2^31 - 1) = 2147483647
		-2^63 < -16 ´ 10^18	(2^63 - 1) < 16 ´ 10^18

Дата добавления: 2014-01-06