Контурные уравнения

Использование узловых уравнений позволяет сократить порядок решаемой системы уравнений до n-1.

Еще одной возможностью снижения порядка решаемой системы уравнений является использование контурных уравнений. Возможность применения таких уравнений обусловлена тем, что по известным токам в хордах, число которых равно числу независимых контуров, можно однозначно определить токи в ветвях дерева графа и, тем самым – токи во всех ветвях.

Если применение узловых уравнений более удобно при отсутствии в схеме ЭДС, то применение контурных уравнений получается более простым при отсутствии задающих токов в узлах, что отвечает схеме замещения, в которой электростанции представлены источниками напряжения, а нагрузки - сопротивлениями.

В этом случае матричное контурное уравнение имеет наиболее простой вид:

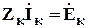, (14)

где Z_к – матрица контурных сопротивлений;

- вектор контурных ЭДС;

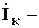вектор контурных токов.

Матрица контурных сопротивлений – это квадратная неособенная матрица порядка К, где К – количество независимых контуров.

Формирование контурных уравнений вида (14) сводится к определению матрицы Z_к. Конкретный вид этой матрицы и степень ее заполненности зависят от выбранной системы независимых контуров. Однако правила формирования матрицы контурных сопротивлений от этого факта не зависят.

Свойства матрицы Z_к:

1. Диагональные элементы Z_ii являются суммами сопротивлений ветвей, входящих в соответствующие контуры. Поэтому они отличны от нуля и, как правило, по абсолютной величине превосходят недиагональные элементы соответ­ст­вующей строки или столбца.

2. Каждый недиагональный элемент 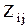равен алгебраической сумме сопротивлений ветвей, одновременно входящих в контуры i и j. Слагаемое этой суммы будет положительным, если направления обхода контуров в пределах данной ветви совпадают, и отрицательным, если не совпадают.

3. Если контуры i и j не имеют общих ветвей, то элемент = 0.

4. Матрица Z_к - симметричная, так как .

Расчет элементов матрицы на ЭВМ производится по формуле

,

Расчет параметров установившегося режима на основе контурных уравнений при отсутствии задающих токов в узлах схемы замещения ведется следующим образом:

1. При известных сопротивлениях и ЭДС ветвей составляется матричное контурное уравнение (14).

2. Уравнение (14) решается относительно контурных токов , которые одновременно являются токами хорд .

3. Определяются токи в ветвях дерева:

.

4. По известным токам ветвей схемы определяются напряжения на ветвях и напряжения узлов относительно базисного:

,

,

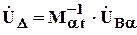где 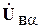- вектор напряжений на ветвях дерева.

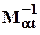- обратная транспонированная подматрица M_{a .}

Дата добавления: 2014-01-06