Решение уравнений состояния итерационными методами

Итерационные методы решения систем линейных алгебраических уравнений позволяют получить значения искомых неизвестных в результате многократного выполнения единообразных шагов, называемых последовательными приближениями или итерациями. В отличие от прямых методов решение можно получить только с заданной конечной точностью, причем с увеличением требуемой точности растет и количество итераций.

В итерационном процессе матрица коэффициентов (А) системы уравнений не подвергается преобразованиям, что позволяет максимально использовать ее слабую заполненность. Однако общее число итераций, как правило, значительно больше порядка n решаемой системы уравнений.

Рассмотрим два итерационных метода решения систем линейных алгебраических уравнений – метод простой итерации и метод Зейделя.

Метод простой итерации. Исходная система линейных уравнений

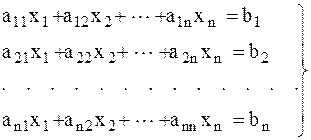
приводится к виду

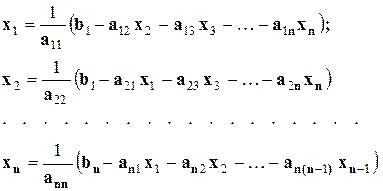(16)

Система уравнений (16) согласно методу простой итерации решается следующим образом:

a) задаются начальными (нулевыми) приближениями неизвестных

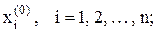
б) значения подставляются в правые части уравнений (16) и тем самым определяются первые приближения неизвестных

в) подстановкой полученных значений 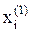находятся вторые приближения 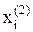и т.д.

Итерационный процесс продолжается до тех пор, пока значения x_i, полученные на двух смежных итерациях, не будут отличаться на величину, меньшую заданной погрешности e.

Проиллюстрируем метод простой итерации, решив систему узловых уравнений:

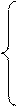
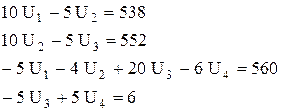(17)

Преобразуем исходную систему:

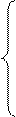U₁ = 53,8 + 0,5 U₂

U₂ = 55,2 + 0,5 U₃ (18)

U₃ = 28 + 0,25 U₁ + 0,2 U₂ + 0,3 U₄

U₄ = 1,2 + U₃

Принимаем начальные приближенные значения узловых напряжений:

Подставив эти значения в правые части уравнений (18), получаем:

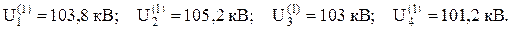
Подставив значения в те же уравнения, вычислим :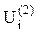

Результаты расчетов по итерациям приведены в таблице 1.

Таблица 1 – Расчет узловых напряжений

Номер итерации, k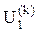
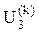
…	103,8 106,4 107,15 107,7375 … 109,1907 109,1907 109,1907	105,2 106,7 107,875 108,8 … 110,7814 110,7814 110,7814	105,35 107,2 108,3275 … 111,1627 111,1628 111,1628	101,2 104,2 106,55 108,4 … 112,3627 112,3628 112,3628

Как следует из приведенных данных, итерационный процесс сошелся с точностью до четырех знаков после запятой за 29 итераций. При уменьшении требуемой точности до 0,1 кВ необходимое количество итераций составляет 14.

Достоинства метода простой итерации:

а) простота реализации алгоритма на ЭВМ;

б) меньшая чувствительность к ошибкам измерений по сравнению с точными методами;

в) ошибки промежуточных расчетов не влияют на конечный результат.

Однако метод простой итерации не всегда обеспечивает возможность получения решения, поскольку не исключена расходимость итерационных процессов.

Как известно, итерационный процесс является сходящимся, если

,

где 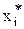- точные решения исходной системы уравнений.

В противном случае процесс называется расходящимся.

Для выполнения условия сходимости итерационного процесса необходимо и достаточно, чтобы собственные значения l_i матрицы С были по абсолютной

величине меньше единицы.

Матрица С может быть определена по формуле

,

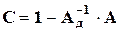где 1 – единичная матрица;

А – матрица коэффициентов исходной системы линейных уравнений;

А_д – диагональная матрица, соответствующая диагональным элементам матрицы А.

Так как расчет собственных значений матрицы С является сложной процедурой, обычно применяют достаточные условия сходимости, формирующиеся непосредственно через элементы матрицы А:

(19)

Таким образом, если диагональные элементы матрицы А по абсолютной величине превышают суммы недиагональных элементов соответствующих строк, то итерационный процесс сходится.

Условия сходимости (или расходимости) итерационного процесса определяются только свойствами матрицы А и не зависят ни от начальных приближений неизвестных , ни от вектора В. Последние два фактора влияют лишь на количество итераций, необходимых для получения решения с заданной точностью.

Как следует из выражения (19), изменение порядка нумерации уравнений, т.е. перестановка строк матрицы А, имеет существенное значение, так как может привести к нарушению необходимых и достаточных условий устойчивости.

С другой стороны, сходимость итерационного процесса может быть обеспечена путем эквивалентного преобразования исходной системы уравнений.

Применительно к решению системы узловых уравнений сходимость итерационного процесса зависит только от свойств матрицы Y_у. Как правило, ее диагональные элементы по абсолютной величине превышают недиагональные элементы соответствующих строк. Однако, поскольку в схемах замещения электрических систем имеются ветви с индуктивными и емкостными проводимостями, достаточные условия сходимости во многих случаях не выполняются.

Так как это лишь достаточные условия, то их невыполнение еще не означает, что итерационный процесс обязательно расходится. В действительности при решении линейных уравнений по методу простой итерации итерационный процесс обычно сходится.

Вместе с тем необходимо иметь в виду, что сама по себе сходимость итерационного процесса не является достаточным основанием для суждения о практическом применении метода.

Метод Зейделя. Этот метод, как и метод простой итерации, базируется на использовании уравнений (16). Однако в отличие от метода простой итерации для вычисления i -й переменной на каждом шаге итерационного процесса используются значения переменных, вычисленных как на предыдущем, так и на данном шаге.

Достаточные условия сходимости метода простой итерации являются достаточными и для метода Зейделя. Если эти условия выполняются, то процесс по методу Зейделя сходится, причем быстрее, чем по методу простой итерации, т.е. при одинаковых начальных приближениях неизвестных и одинаковой заданной точности решение по методу Зейделя получается за меньшее число итераций.

Опыт решения линейных уравнений состояния электрической системы показывает, что и в тех случаях, когда достаточные условия сходимости не выполняются, метод Зейделя обычно характеризуется более быстрой сходимостью по сравнению с методом простой итерации.

Произведем решение предыдущей задачи по методу Зейделя.

В расчетах используются уравнения (18).

Принимаем те же начальные значения узловых напряжений, что и в преды-

дущих расчетах:

П е р в а я и т е р а ц и я

В т о р а я и т е р а ц и я

Результаты остальных расчетов приведены в таблице 2

Таблица 2 – Решение узловых уравнений по методу Зейделя

Номер итерации, k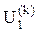
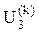
…	103,8 106,4 107,6475 108,399 … 109,1907 109,1907 109,1907	105,2 107,695 109,198 109,9551 … 110,7813 110,7814 110,7814	104,99 107,996 109,5103 110,3039 … 111,1627 111,1628 111,1628	106,19 109,196 109,7103 111,5039 … 112,3627 112,3628 112,3628

Таким образом, метод Зейделя сходится быстрее, чем метод простой итера-

ции. Результаты расчетов полностью совпадают.

Дата добавления: 2014-01-06