Метод Ньютона

Метод Ньютона весьма эффективен для решения нелинейных алгебраических и трансцендентных уравнений. Его основное достоинство состоит в том, что при сравнительно несложной схеме вычисления он обладает быстрой сходимостью. Метод Ньютона универсален и пригоден не только для расчета установившихся режимов электрических систем, но и для решения других задач.

Идея метода Ньютона состоит в последовательной замене на каждой итерации нелинейной системы уравнений некоторой линейной, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение.

Поясним идею этого метода на примере решения нелинейного уравнения с одним неизвестным

. (24)

Решение этого уравнения - это точка, в которой кривая y (x) проходит через нуль (рис. 8).

Зададим начальное приближение .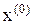

Заменим уравнение (24) в окрестности точки 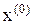линейным уравнением

(25)

где -значениепроизводной в точке x⁽⁰⁾.

Левая часть уравнения (25) представляет собой два первых члена разложения функции в ряд Тейлора.

Решим линейное уравнение (25) и определим поправку Dx⁽¹⁾ к начальному приближению:

.

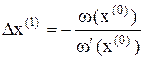За новое приближение неизвестной величины принимаем x⁽¹⁾ = x⁽⁰⁾ + Dx⁽¹⁾.

Аналогично определяются следующие приближения:

.

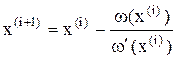Итерационный процесс сходится, если функция становится близкой к нулю. Сходимость считается достигнутой, если величина небаланса становится меньше заданной:

При выполнении расчетов необходимо иметь в виду, что контроль сходимости по величине поправки Dx⁽ⁱ⁾ может привести к неверным результатам.

Как следует из рисунка 8, каждый шаг метода Ньютона сводится к замене кривой w(x) прямой линией, которая является касательной к этой кривой в точке x = x⁽ⁱ⁾. Поэтому метод Ньютона называют также методом касательных. Приближение x⁽ⁱ⁺¹⁾ есть точка пересечения касательной к кривой в точке x = x⁽ⁱ⁾ с осью x.

Рассмотрим решение по методу Ньютона системы нелинейных алгебраических уравнений

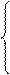
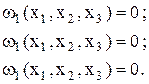(26)

Если использовать вектор-столбец X и вектор-функцию W(X),

где

X=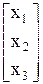, W(X) = ,

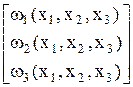то систему уравнений (26) можно записать в матричном виде:

W(X) = 0.

Пусть - начальные приближения неизвестных. Заменим каждое из нелинейных уравнений (26) линейным, полученным разложением в ряд Тейлора. Например, первое уравнение после линеаризации будет иметь следующий вид:

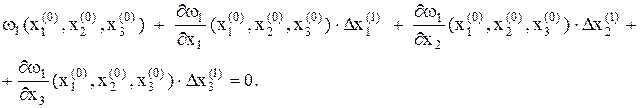
Аналогичный вид имеют уравнения для функций w₂ и w₃.

Запишем матрицу Якоби, т.е. матрицу частных производных:

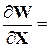
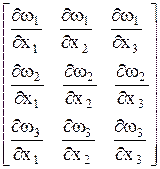(27)

Тогда систему линеаризованных уравнений можно записать в матричном виде следующим образом:

.

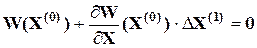Перенесем вектор-функцию в правую часть уравнения

(28)

Таким образом, получена система линейных уравнений, в которой неизвестными являются элементы вектора поправок 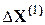, а элементы матрицы Якоби 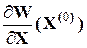играют ту же роль, что и коэффициенты в обычных линейных уравнениях.

Если определитель матрицы Якоби (якобиан) не равен нулю, уравнение (28) может быть решено относительно .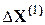

Решим линейную систему (28) любым из ранее рассмотренных методов и

определим поправки. Затем найдем первое приближение переменных:

X ⁽¹⁾ = X ⁽⁰⁾ + DX ⁽¹⁾.

Каждый шаг итерационного процесса состоит из решения линейной системы

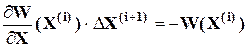
и определения следующего приближения неизвестных

X ⁽ⁱ⁺¹⁾ = X ⁽ⁱ⁾ + DX ⁽ⁱ⁺¹⁾.

Контроль сходимости осуществляется по вектору небалансов, т.е. условие

w_k (X ⁽ⁱ⁾)

должно выполняться для всех небалансов (невязок).

Метод Ньютона обеспечивает быструю сходимость, и уже первое приближение, как правило, дает удовлетворительный для практики результат. Несмотря на это, метод Ньютона не мог претендовать на практическое применение в задачах расчета электрических сетей до использования ЭВМ из-за трудоемкости вы­числения матрицы производных.

Важнейшее преимущество метода Ньютона – возможность комплексной оптимизации установившихся режимов.

Метод Ньютона сходится значительно быстрее и надежнее метода Зейделя, а также, как правило, быстрее и надежнее, чем при использовании метода Гаусса, матрицы узловых проводимостей и других методов, суть которых состоит в решении на каждом шаге линейных уравнений узловых напряжений.

Дата добавления: 2014-01-06