Линейные групповые коды

Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.

Для двоичных кодов в качестве линейной операции используется сложение по модулю 2.

Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.

Свойство линейных кодов:

сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.

Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами.

Свойство группового кода:

минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонент.

Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2. Таким образом, для данного группового кода

W_min =d_0.

Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода k и r. Число строк матрицы равно k, число столбцов равно

n = k + r:

Коды, порождаемые этими матрицами, известны как (n,k)-коды, соответствующие им матрицы называют порождающими (производящими, образующими).

Порождающая матрица P может быть представлена двумя матрицами U_k и H_r (информационной и проверочной). Число столбцов матрицы H_r равно r, число столбцов матрицы U_k равно k

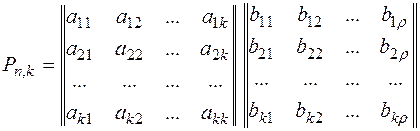
Теорией и практикой установлено, что в качестве матрицы U_k удобно брать единичную матрицу в канонической форме

Для кодов с d_0­ = 2 производящая матрица P имеет вид

Во всех комбинациях кода построенного при помощи такой матрицы, четное число единиц.

Для кодов с d₀ ³ 3 порождающая матрица не может быть представлена в форме, общей для всех кодов с данным d_{0 ­.} Вид матрицы зависит от конкретных требований к порождающему коду. Этими требованиями могут быть либо минимум корректирующих разрядов, либо максимальная простота аппаратуры.

Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.

Для кодов d₀ = 3 соотношения n и k следующие: (3; 1), (7; 4),
(15; 11), (31; 26), (63; 57) и так далее.

Строчки образующей матрицы P представляют собой k комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения и исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы H_r, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают полный вектор корректирующего кода. Аналогичную процедуру проделывают со второй, третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита.

Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом

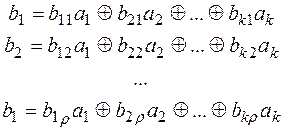
или

.

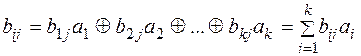В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом

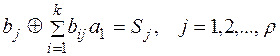
Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным рядом b₁ входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы H_r; во вторую проверку входит второй проверочный разряд b₂ и информационные разряды, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода r.

В результате осуществления проверок образуется проверочный вектор S₁, S₂,..., S_r, который называется синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один единственный проверочный вектор.

Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н’, которая представляет собой транспонированную матрицу H_r, дополненной единичной матрицей I_r, число столбцов которой равно число проверочных разрядов кода

Н’ = úç H_r^ТI_r úç.

Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н’.

Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.

Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы A_i. В первом столбце второй строки размещается вектор a₁, вес которого равен 1.

Остальные позиции второй строки заполняются векторами, полученными в результате суммирования по модулю 2 вектора a₁ с А _i, расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор a₂, вес которого также равен 1, однако, если вектор a₁ содержит единицу в первом разряде, то a₂ - во втором. В остальные позиции третьей строки записывают суммы А_i и a₂.

Аналогично поступают до тех пор, пока не будут просуммированы с векторами А_i все векторы a_j весом 1, с единицей в каждом из n разрядов. Затем суммируются по модулю 2 векторы a_j, весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора a_j определяет число исправляемых ошибок. Число векторов a_j определяется возможным числом неповторяющихся синдромов и равно 2^r-1 (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор a_j. Векторы a_j есть векторы ошибок, которые могут быть исправлены данным групповым кодом.

По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации А_i с вектором ошибки a_j, т. е. к определенной строке кодовой таблицы 5.8.

Таблица 5.8 - Кодовая таблица групповых кодов

a	A1	A2	...	A(2^k-1)
a1	a1ÅA1	a2ÅA2	...	a1ÅA(2^k-1)
a2	a2ÅA1	a2ÅA2	...	a2ÅA(2^k-1)
...	...	...	...	...
a(2^r-1)	a­(2 ^r- 1)ÅA1	a(2^r^­-1)­ÅA2	...	a(2^r-1)ÅA(2^k-1)

Принятая кодовая комбинация A^x_n сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов.

Векторы a₁, a₂,...,a₍₂^r_-1) не должны быть равными ни одному из векторов А₁, А₂,..., А₍₂^r_-1), в противном случае в таблице появились бы нулевые векторы.

Пример.

Построить кодовую таблицу, при помощи которой обнаруживаются и исправляются все одиночные ошибки и некоторые ошибки кратностью r + 1, в информационной части кода (11,7), построенного по матрице

Решение.

Используя таблицу 5.8, строим кодовую таблицу 5.9 для кодов, построенных по данной матрице P, кодовые комбинации строятся путем добавления к четырехразрядным комбинациям натурального двоичного кода корректирующих разрядов по правилу, описанному выше.

Определяем систему проверок исходя из матрицы H_r

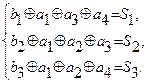
Находим вид синдрома для каждой строки таблицы. Для этого достаточно произвести проверки для кодовых комбинаций любого столбца кодовой таблицы.

Для нашего примера возьмем столбец A₃ .

Таблица 5.9 – Пример таблицы для столбца А₃

№	e	A1	A2	A3	A4	A5	A6	A7
№	A8	A9	A10	A11	A12	A13	A14	A15

1) 0 1 0 0 1 0 0

2) 1 0 0 0 1 0 0

3) 1 1 1 0 1 0 0

4) 1 1 0 1 1 0 0

5) 0 0 0 0 1 0 0

6) 0 1 0 1 1 0 0

7) 0 1 1 0 1 0 0

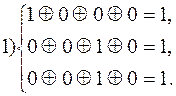
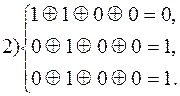
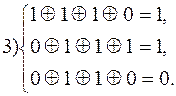
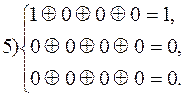
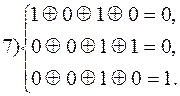
Таким образом вектору ошибки a₁ соответствует синдром 1 1 1

__________ “____________ a₂ ________ “_________ 0 1 1

__________ “____________ a₃ ________ “_________ 1 1 0

__________ “____________ a₄ ________ “_________ 1 0 1

__________ “____________ a₅ ________ “_________ 1 0 0

__________ “____________ a₆ ________ “_________ 0 1 0

__________ “____________ a₇ ________ “_________ 0 0 1

Предположим, приняты комбинации 1011001, 1000101, 0001100, 0000001 и 1010001. Производим проверки

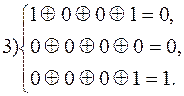
Синдром первой принятой комбинации - 101, значит вектор ошибки а₄ = 0001000, исправление ошибки производится заменой символа в четвертом разряде принятой комбинации на обратный. Истинная комбинация - А₅, так как принятая комбинация находится в шестом столбце таблицы в строке, соответствующей синдрому 101.

Синдром второй принятой комбинации - 010, находим ее в шестой строке (010 соответствует а₆) и в девятом столбце. Истинная комбинация А₈ = 0001101, т.е. исправлена двойная ошибка.

Синдром третьей принятой комбинации - 001 соответствует а₇, истинная комбинация А₁₃.

Синдром четвертой из принятых комбинаций - 001 также соответствует а₇, но принятую комбинацию мы находим в шестом столбце таблицы, следовательно, истинная комбинация - А₅.

Синдром шестой принятой комбинации - 000. Ошибки нет.

Дата добавления: 2014-01-06