Код Хэмминга

Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т.е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.

Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных комбинаций N = 2^k. При помощи формул

,

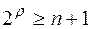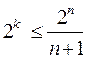
вычисляются k и r. Соотношения между n, k и r для кода Хэмминга представлены в таблице

Таблица 5.10 – Соотношения между n, k, r в коде Хэмминга

n	k	r	n	k	r

Зная основные параметры корректирующего кода, определяют: какие позиции кода будут информационными, а какие проверочными. Как показала практика, номера контрольных символов удобно выбирать по закону 2ⁱ, где i = 0, 1, 2 и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.

Затем определяют значения проверочных разрядов (0 или 1), руководствуясь следующим правилом: сумма единиц на проверочных позициях должна быть четной. Если эта сумма четна, то значение контрольного разряда - 0, в противном случае - 1.

Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы

n = k + r.

Первой строке соответствует проверочный символ a₁ второй - a₂ и т.д., как показано в таблице.

Таблица 5.11 – Ряд натуральных чисел в двоичном коде

n	Двоичный код	Провероч-ные коэффициенты	n	Двоичный Код	провероч-ные коэффициенты
	0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0	а1 a2 a3 a4 a5 a6		0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1	a7 a8 a9 a10 a11

Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу:

в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. a₁, a₃,, a₅ , a₇ , a₉ ,a₁₁ и т.д.;

во вторую - коэффициенты, содержащие 1 во втором разряде, т.е. и т.д. a₂, a₃,, a₆, a₇, a₁₀,a₁₁ и т.д.;

в третью проверку - коэффициенты, которые содержат 1 в третьем разряде, и т.д.

Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок.

Таблица 5.12 – Таблица проверок

№ проверки	Проверочные позиции	№ провероч-ного разряда
	1, 3, 5, 7, 9, 11... 2, 3, 6, 7, 10, 11, 14, 15, 18,19, 22, 23, 26, 27, 30, 31... 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28, 29, 30, 31... 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28, 29, 30, 31, 40, 41, 42, 43, 44, 45, 46...

Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также порядок следования разрядов в полученном двоичном коде.

Если в принятом коде есть ошибка, то результаты проверок по контрольным позициям образуют двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции на противоположный.

Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации была всегда четной. Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки.

Пример.

Построить код Хэмминга для информационной комбинации 0101. Показать процесс обнаружения ошибки.

Решение.

Количество информационных разрядов k = 4. Находим значения общей длины кодовой комбинации и число контрольных символов: r = 3 и n = 7. Так как общее количество символов кода n = 7, то контрольные коэффициенты займут три позиции: 1, 2 и 4.

Корректирующий код без значений контрольных коэффициентов будет иметь вид:

b₁ b₂ 0 b₃ 1 0 1.

Пользуясь таблицей проверочных позиций, определяем значения контрольных коэффициентов.

Первая проверка: сумма П₁ Å П₃ Å П₅ Å П₇ должна быть четной, а сумма b₁ Å 0 Å 1Å 1 будет четной при b₁ = 0.

Вторая проверка: сумма П₂ Å П₃ Å П₆ Å П₇ должна быть четной, а сумма b₂ Å 0 Å 0 Å 1 будет четной при b₂ = 1.

Третья проверка: сумма П₄ Å П₅ Å П₆ Å П₇ должна быть четной, а сумма b₃ Å 1Å 0 Å 1 будет четной при b₃ = 0.

Окончательно корректирующий код принимает вид:

0 1 0 0 1 0 1.

Предположим, в результате искажений в канале связи вместо 0100101 было принято 0100111. Для обнаружения ошибки производим контроль на четность, аналогичные проверкам при выборе контрольных коэффициентов.

Первая проверка: сумма П₁ Å П₃ Å П₅ Å П₇ = 0 Å 0 Å 1Å 1 четна. В младший разряд номера ошибочной позиции записываем 0.

Вторая проверка: сумма П₂ Å П₃ Å П₆ Å П₇ = 1 Å 0 Å 1Å 1 нечетна. Во второй разряд номера ошибочной позиции записываем 1.

Третья проверка: сумма П₄ Å П₅ Å П₆ Å П₇ = 0 Å 1 Å 1Å 1 нечетна. В третий разряд номера ошибочной позиции записываем 1.

Номер ошибочной позиции 110₂ = 6₁₀. Следовательно, символ шестой позиции следует изменить на обратный.

Дата добавления: 2014-01-06