Множества. Множеством Sназывается объединение в одно целое объектов, хорошо различимых нашей мыслью или интуицией

ТЕОРИЯ МНОЖЕСТВ.

Множеством S называется объединение в одно целое объектов, хорошо различимых нашей мыслью или интуицией. Эти объекты называется элементами множества S. Такое интуитивное определение дал немецкий математик Г. Кантор. В данном определении важны следующие два момента:

1. Множество- это нечто, состоящее из хорошо различимых объектов.

2. Это нечто мыслится как единое целое.

Множества бывают конечными и бесконечными, Количество элементов в конечном множестве называется мощностью множества. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. Множество, включающее в себя в се рассматриваемые множества, называется универсальным множеством или универсумом и обозначается U. Символом Î обозначается отношение принадлежности. Запись xÎC означает, что элемент х принадлежит множеству Х. Если элемент х не принадлежит множеству Х, то пишут хÏХ.

Множества могут быть заданы следующими способами:

1. перечислением (списком своих элементов);

2. описанием свойств, которыми должны обладать его элементы;

3. порождающей процедурой.

ПРИМЕР

Множество экзаменационных оценок может быть задано:

1. перечислением А={2; 3; 4; 5}

2. описанием свойств: А={a| a- экзаменационная оценка}

3. порождающей процедурой: А={а| а=2+i, i=}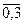

Подмножеством множества А называется множество В, если любой элемент множества В принадлежит множеству А:

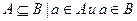(1)

Символом Í обозначается отношение включения. Запись АÍВ означает множество А является подмножеством множества В.

Не следует смешивать отношение принадлежности Î и отношение включения Í. Отношение принадлежности применяется к элементам множества, а отношение включения к множествам. Хотя 1Î{1},{1}Î{{1}}, не верно, что 1Î{{1}}, так как единственным элементом множества {{1}} является {1}.

Если АÍB и A¹B, то AÌB, то есть множество А строго включено в множество В. Символ Ì называется строгим включением.

Дата добавления: 2014-01-06