Эмпирическая функция распределения

Лекция 13. Понятие о статистических оценках случайных величин

Пусть известно статистическое распределение частот количественного признака X. Обозначим через число наблюдений, при которых наблюдалось значение признака, меньшее x и через n – общее число наблюдений. Очевидно, относительная частота события X < x равна 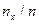и является функцией x. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения x относительную частоту события X < x. Таким образом, по определению ,где - число вариант, меньших x, n – объем выборки.

В отличие от эмпирической функции распределения выборки, функцию распределения 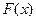генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция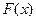определяет вероятность события X < x, тогда как эмпирическая – относительную частоту этого же события.

При росте n относительная частота события X < x, т.е. стремится по вероятности к вероятности 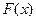этого события. Иными словами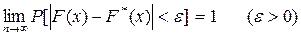

Свойства эмпирической функции распределения:

1) Значения эмпирической функции принадлежат отрезку [0,1]

2) - неубывающая функция

3) Если - наименьшая варианта, то = 0 при 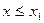, если 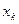- наибольшая варианта, то =1 при .

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример. Построим эмпирическую функцию по распределению выборки:

Варианты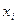
Частоты

Найдем объем выборки: 12+18+30=60. Наименьшая варианта равна 2, поэтому =0 при x £ 2. Значение x<6, т.е. , наблюдалось 12 раз, следовательно, =12/60=0,2 при 2< x £6. Аналогично, значения X < 10, т.е. и наблюдались 12+18=30 раз, поэтому =30/60 =0,5 при 6< x £10. Так как x=10 – наибольшая варианта, то =1 при x> 10. таким образом, искомая эмпирическая функция имеет вид:

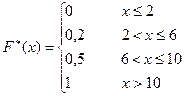
Важнейшие свойства статистических оценок

Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр l.

Обычно имеются лишь данные выборки, например значения количественного признака 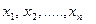, полученные в результате n независимых наблюдений. Рассматривая 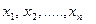как независимые случайные величины можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое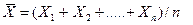

Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенности и состоятельности оценки.

Пусть 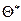- статистическая оценка неизвестного параметра 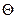теоретического распределения. Пусть по выборке объема n найдена оценка . Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку 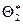. Повторяя опыт многократно, получим различные числа 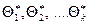. Оценку 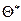можно рассматривать как случайную величину, а числа 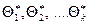- как ее возможные значения.

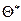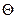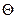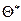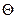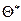Если оценка дает приближенное значение с избытком, т.е. каждое число больше истинного значения то, как следствие, математическое ожидание (среднее значение) случайной величины больше, чем :. Аналогично, если дает оценку с недостатком, то .

Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. Если, напротив, , то это гарантирует от систематических ошибок.

Несмещенной называют статистическую оценку 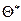, математическое ожидание которой равно оцениваемому параметру 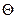при любом объеме выборки .

Смещенной называют оценку, не удовлетворяющую этому условию.

Несмещенность оценки еще не гарантирует получения хорошего приближения для оцениваемого параметра, так как возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия может быть значительной. В этом случае найденная по данным одной выборки оценка, например , может оказаться значительно удаленной от среднего значения ,а значит, и от самого оцениваемого параметра.

Эффективной называют статистическую оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называется статистическая оценка, которая при n®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®¥ стремится к нулю, то такая оценка оказывается и состоятельной.

Дата добавления: 2014-01-06