Выборочные среднее и дисперсия

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Выборочным средним 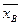называют среднее арифметическое значение признака выборочной совокупности. Если все значения 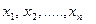признака выборки объема n различны, то .

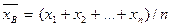Если значения признака 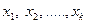имеют частоты 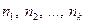соответственно, причем 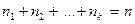, то .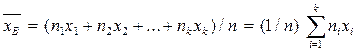

Выборочное среднее, найденное по данным одной выборки, равно определенному числу. При извлечении других выборок того же объема выборочное среднее будет меняться от выборки к выборке. То есть выборочное среднее можно рассматривать как случайную величину и говорить о его распределениях (теоретическом и эмпирическом) и о числовых характеристиках этого распределения (например, о математическом ожидании и дисперсии).

Для охарактеризования рассеяния наблюдаемых значений количественного признака выборки вокруг среднего значения 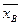вводится выборочная дисперсия. Выборочной дисперсией 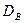называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 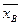. Если все значения 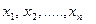признака выборки объема n различны, то .

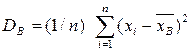Если значения признака 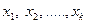имеют частоты 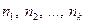соответственно, причем 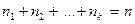, то .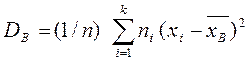

Аналогично выборочным среднему и дисперсии определяются генеральные среднее и дисперсия, характеризующие генеральную совокупность в целом. Для расчета этих характеристик достаточно в вышеприведенных соотношениях заменить объем выборки n на объем генеральной совокупности N.

Фундаментальное значение для практики имеет нахождение среднего и дисперсии признака генеральной совокупности по соответствующим известным выборочным параметрам. Можно показать, что выборочное среднее является несмещенной состоятельной оценкой генерального среднего. В то же время, несмещенной состоятельной оценкой генеральной дисперсии оказывается не выборочная дисперсия 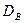, а так называемая “ исправленная ” выборочная дисперсия, равная .

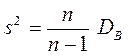Таким образом, в качестве оценок генерального среднего и дисперсии в математической статистике принимают выборочнее среднее и исправленную выборочную дисперсию.

Надежность и доверительный интервал.

До сих пор мы рассматривали точечные оценки, т.е. такие оценки, которые определяются одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. В связи с этим при небольшом объеме выборки пользуются интервальными оценками.

Интервальной называют оценку, определяющуюся двумя числами – концами интервала. Пусть найденная по данным выборки статистическая характеристика 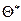служит оценкой неизвестного параметра 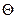. Очевидно, 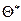тем точнее определяет параметр 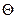, чем меньше абсолютная величина разности 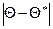. Другими словами, есл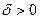и и 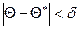, то чем меньше d, тем точнее оценка. Таким образом, положительное число d характеризует точность оценки.

Статистические методы не позволяют утверждать, что оценка 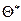удовлетворяет неравенству 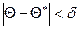; можно говорить лишь о вероятности, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки 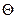по 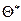называют вероятность g, с которой осуществляется неравенство 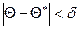. Обычно надежность оценки задается заранее, причем в качестве g берут число, близкое к единице – как правило 0,95; 0,99 или 0,999.

Пусть вероятность того, что 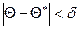равна g:.

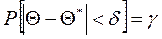Заменим неравенство 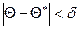равносильным ему двойным неравенством

.

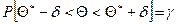Это соотношение следует понимать так: вероятность того, что интервал 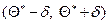заключает в себе (покрывает) неизвестный параметр Q, равна.

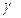Таким образом, доверительным называют интервал 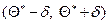, который покрывает неизвестный параметр с заданной надежностью .

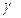Величину 1 - g = a называют уровнем значимости или вероятностью ошибки.

Для построения интервальной оценки параметра необходимо знать закон его распределения как случайной величины

Лекция 14. Доверительные интервалы для математического ожидания и дисперсии

1. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения известно. Требуется оценить неизвестное математическое ожидание 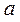по выборочному среднему 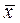. Найдем доверительные интервалы, покрывающие параметр a с надежностью .

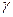Будем рассматривать выборочное среднее 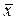как случайную величину 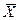(т.к. 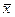меняется от выборки к выборке) и выборочные значения 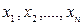- как одинаково распределенные независимые случайные величины 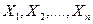(эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно 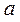и среднее квадратическое отклонение - s. Так как случайная величина X распределена нормально, то и выборочное среднее 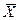также распределено нормально. Параметры распределения 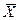равны .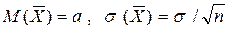

Потребуем, чтобы выполнялось соотношение ,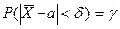

где 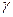- заданная надежность. Используем формулу .

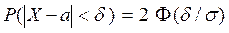Заменим X на 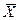и s на 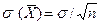и получим

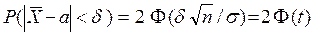
где 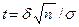. Выразив из последнего равенства 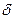, получим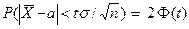

Так как вероятность P задана и равна 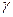, окончательно имеем

.

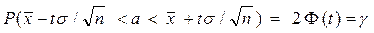Таким образом, с надежностью 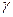можно утверждать, что доверительный интервал 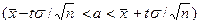покрывает неизвестный параметр a, причем точность оценки равна .

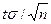Число 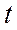определяется из равенства 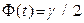; по таблице функции Лапласа находят аргумент 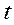, которому соответствует значение функции Лапласа, равное .

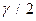Отметим два момента: 1) при возрастании объема выборки n число 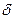убывает и, следовательно, точность оценки увеличивается, 2) увеличение надежности оценки 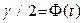приводит к увеличению 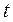(так как функция Лапласа возрастающая функция) и, следовательно, к возрастанию 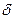, то есть увеличение надежности оценки влечет за собой уменьшение ее точности.

Если требуется оценить математическое ожидание с наперед заданной точностью 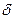и надежностью 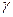, то минимальный объем выборки, который обеспечит эту точность, находят по формуле

,

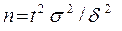следующей из равенства .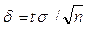

2. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.

Оказывается, что по данным выборки можно построить случайную величину ,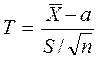

которая имеет распределение Стьюдента с 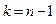степенями свободы. В последнем выражении - 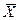- выборочное среднее, 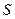- исправленное среднее квадратическое отклонение, 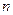- объем выборки; возможные значения случайной величины T мы будем обозначать через t. Плотность распределения Стьюдента имеет вид

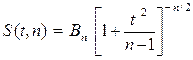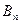, где некоторая постоянная, выражающаяся через гамма – функции.

Несколько слов о распределении Стьюдента. Пусть 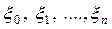- независимые стандартные нормальные величины. Тогда случайная величина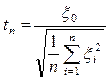

имеет распределение Стьюдента (В. Госсет) с 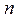степенями свободы. При росте числа степеней свободы распределение Стьюдента стремится к нормальному распределению и уже при 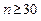использование нормального распределения дает хорошие результаты.

Как видно, распределение Стьюдента определяется параметром n – объемом выборки (или, что то же самое – числом степеней свободы 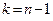) и не зависит от неизвестных параметров 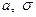. Поскольку 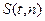- четная функция от t, то вероятность выполнения неравенства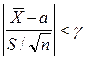

определяется следующим образом:.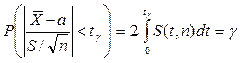

Заменив неравенство в круглых скобках двойным неравенством, получим выражение для искомого доверительного интервала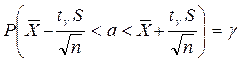

Итак, с помощью распределения Стьюдента найден доверительный интервал 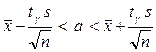, покрывающий неизвестный параметр a с надежностью 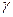. По таблице распределения Стьюдента и заданным n и 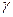можно найти 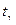и используя найденные по выборке 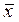и 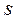,, можно определить доверительный интервал.

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 16 найдены генеральное среднее 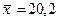и исправленное среднее квадратическое отклонение 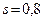. Требуется оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем 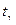по таблице распределения Стьюдента, используя значения 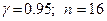. Этот параметр оказывается равным 2,13. Найдем границы доверительного интервала:

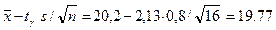
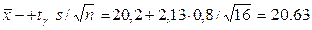
То есть с надежностью 0,95 неизвестный параметр a заключен в доверительном интервале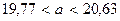

Можно показать, что при возрастании объема выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо него пользоваться нормальным распределением. При малых n это приводит к значительным ошибкам.

3. Доверительный интервал для оценки среднего квадратического отклонения s нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение s по исправленному выборочному среднему квадратическому отклонению s. Найдем доверительные интервалы, покрывающие параметр s с заданной надежностью .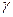

Потребуем, чтобы выполнялось соотношение

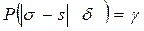или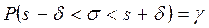

Преобразуем двойное неравенство 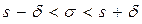в равносильное неравенство 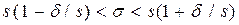и обозначим d / s = q. Имеем 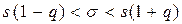(A)

и необходимо найти q. С этой целью введем в рассмотрение случайную величину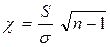

Оказывается, величина 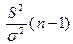распределена по закону 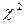с n – 1 степенями свободы.

Несколько слов о распределении хи-квадрат. Если 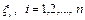- независимые стандартные нормальные величины, то говорят, что случайная величина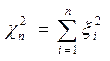

имеет распределение хи-квадрат с 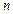степенями свободы.

Плотность распределения c имеет вид

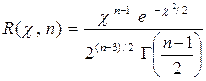
Это распределение не зависит от оцениваемого параметра s, а зависит только от объема выборки n.

Преобразуем неравенство (A) так, чтобы оно приняло вид 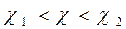. Вероятность этого неравенства равна заданной вероятности 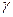, т.е. .

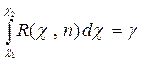Предполагая, что q < 1, перепишем (A) в виде

,

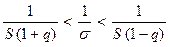далее, умножим все члены неравенства на :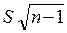

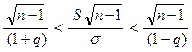или .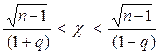

Вероятность того, что это неравенство, а также равносильное ему неравенство (A) будет справедливо, равна

.

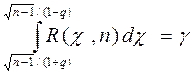Из этого уравнения можно по заданным 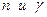найти 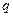, используя имеющиеся расчетные таблицы. Вычислив по выборке 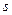и найдя по таблице 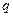, получим искомый интервал (A1), покрывающий s с заданной надежностью .

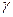Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено исправленное среднее квадратическое отклонение s = 0.8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение s с надежностью 0,95.

Решение. По заданным 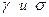по таблице находим значение q = 0.32. Искомый доверительный интервал есть

.

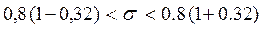Мы предполагали, что q < 1. Если это не так, то мы придем к соотношениям

,

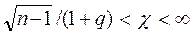и значение q >1 может быть найдено из уравнения

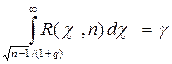
Лекция 14. Доверительные интервалы для математического ожидания и дисперсии

1. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения известно. Требуется оценить неизвестное математическое ожидание 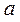по выборочному среднему 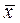. Найдем доверительные интервалы, покрывающие параметр a с надежностью .

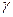Будем рассматривать выборочное среднее 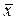как случайную величину 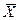(т.к. 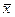меняется от выборки к выборке) и выборочные значения 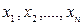- как одинаково распределенные независимые случайные величины 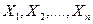(эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно 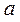и среднее квадратическое отклонение - s. Так как случайная величина X распределена нормально, то и выборочное среднее 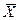также распределено нормально. Параметры распределения 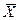равны .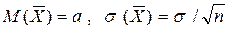

Потребуем, чтобы выполнялось соотношение ,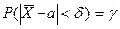

где 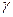- заданная надежность. Используем формулу .

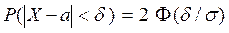Заменим X на 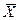и s на 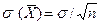и получим

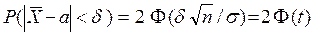
где 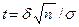. Выразив из последнего равенства 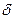, получим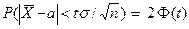

Так как вероятность P задана и равна 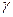, окончательно имеем

.

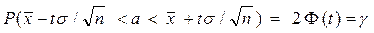Таким образом, с надежностью 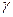можно утверждать, что доверительный интервал 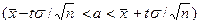покрывает неизвестный параметр a, причем точность оценки равна .

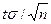Число 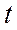определяется из равенства 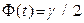; по таблице функции Лапласа находят аргумент 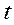, которому соответствует значение функции Лапласа, равное .

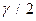Отметим два момента: 1) при возрастании объема выборки n число 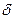убывает и, следовательно, точность оценки увеличивается, 2) увеличение надежности оценки 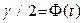приводит к увеличению 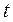(так как функция Лапласа возрастающая функция) и, следовательно, к возрастанию 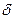, то есть увеличение надежности оценки влечет за собой уменьшение ее точности.

Если требуется оценить математическое ожидание с наперед заданной точностью 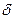и надежностью 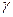, то минимальный объем выборки, который обеспечит эту точность, находят по формуле

,

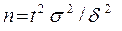следующей из равенства .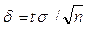

4. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание с помощью доверительных интервалов.

Оказывается, что по данным выборки можно построить случайную величину ,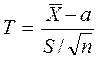

которая имеет распределение Стьюдента с 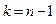степенями свободы. В последнем выражении - 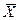- выборочное среднее, 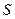- исправленное среднее квадратическое отклонение, 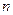- объем выборки; возможные значения случайной величины T мы будем обозначать через t. Плотность распределения Стьюдента имеет вид

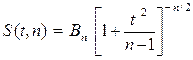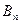, где некоторая постоянная, выражающаяся через гамма – функции.

Несколько слов о распределении Стьюдента. Пусть 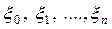- независимые стандартные нормальные величины. Тогда случайная величина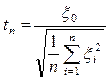

имеет распределение Стьюдента (В. Госсет) с 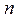степенями свободы. При росте числа степеней свободы распределение Стьюдента стремится к нормальному распределению и уже при 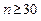использование нормального распределения дает хорошие результаты.

Как видно, распределение Стьюдента определяется параметром n – объемом выборки (или, что то же самое – числом степеней свободы 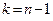) и не зависит от неизвестных параметров 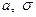. Поскольку 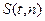- четная функция от t, то вероятность выполнения неравенства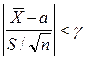

определяется следующим образом:.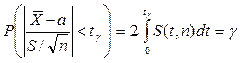

Заменив неравенство в круглых скобках двойным неравенством, получим выражение для искомого доверительного интервала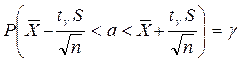

Итак, с помощью распределения Стьюдента найден доверительный интервал 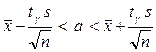, покрывающий неизвестный параметр a с надежностью 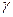. По таблице распределения Стьюдента и заданным n и 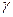можно найти 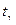и используя найденные по выборке 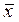и 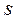,, можно определить доверительный интервал.

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 16 найдены генеральное среднее 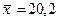и исправленное среднее квадратическое отклонение 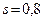. Требуется оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем 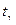по таблице распределения Стьюдента, используя значения 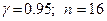. Этот параметр оказывается равным 2,13. Найдем границы доверительного интервала:

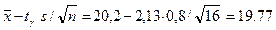
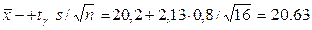
То есть с надежностью 0,95 неизвестный параметр a заключен в доверительном интервале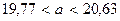

Можно показать, что при возрастании объема выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо него пользоваться нормальным распределением. При малых n это приводит к значительным ошибкам.

3. Доверительный интервал для оценки среднего квадратического отклонения s нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально и требуется оценить неизвестное генеральное среднее квадратическое отклонение s по исправленному выборочному среднему квадратическому отклонению s. Найдем доверительные интервалы, покрывающие параметр s с заданной надежностью .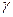

Потребуем, чтобы выполнялось соотношение

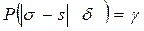или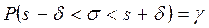

Преобразуем двойное неравенство 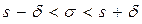в равносильное неравенство 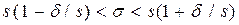и обозначим d / s = q. Имеем 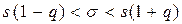(A)

и необходимо найти q. С этой целью введем в рассмотрение случайную величину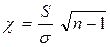

Оказывается, величина 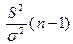распределена по закону 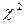с n – 1 степенями свободы.

Несколько слов о распределении хи-квадрат. Если 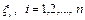- независимые стандартные нормальные величины, то говорят, что случайная величина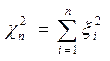

имеет распределение хи-квадрат с 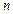степенями свободы.

Плотность распределения c имеет вид

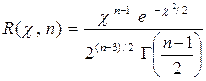
Это распределение не зависит от оцениваемого параметра s, а зависит только от объема выборки n.

Преобразуем неравенство (A) так, чтобы оно приняло вид 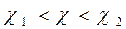. Вероятность этого неравенства равна заданной вероятности 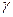, т.е. .

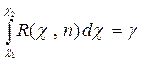Предполагая, что q < 1, перепишем (A) в виде

,

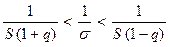далее, умножим все члены неравенства на :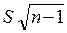

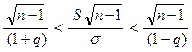или .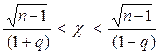

Вероятность того, что это неравенство, а также равносильное ему неравенство (A) будет справедливо, равна

.

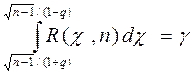Из этого уравнения можно по заданным 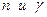найти 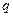, используя имеющиеся расчетные таблицы. Вычислив по выборке 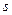и найдя по таблице 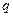, получим искомый интервал (A1), покрывающий s с заданной надежностью .

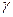Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено исправленное среднее квадратическое отклонение s = 0.8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение s с надежностью 0,95.

Решение. По заданным 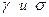по таблице находим значение q = 0.32. Искомый доверительный интервал есть

.

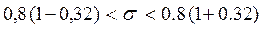Мы предполагали, что q < 1. Если это не так, то мы придем к соотношениям

,

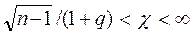и значение q >1 может быть найдено из уравнения

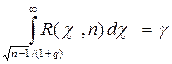
Лекция 15. Проверка статистических гипотез. Нулевая и альтернативная гипотезы, статистический критерий. Ошибки первого и второго рода. Этапы проверки статистической гипотезы. Критерий согласия Пирсона о виде распределения.

На прошлой лекции мы рассматривали задачу построения доверительных интервалов для неизвестных параметров генеральной совокупности. Сегодня мы продолжим изучение основных задач математической статистики и перейдем к вопросу проверки статистических гипотез.

Проверка статистических гипотез представляет собой важнейший этап процесса принятия решения в управленческой деятельности, позволяя проводить подготовительный этап предстоящих действий с учетом реальных характеристик процесса производства, контроля качества продукции, коммерческой деятельности, и т.п.

Как известно, закон распределения определяет количественные характеристики генеральной совокупности.

Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (например, А), то выдвигают гипотезу: генеральная совокупность распределена по закону А. В этой гипотезе речь идет о виде предполагаемого распределения.

Часто закон распределения известен, но неизвестны его параметры. Если есть основания предположить, что неизвестный параметр 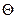равен определенному значению 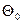, то может выдвигаться гипотеза 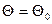. В этой гипотезе речь идет о предполагаемой величине параметра известного распределения.

Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и т. д.

Приведем несколько задач, которые могут быть решены с помощью проверки статистических гипотез.

1. Используется два метода измерения одной и той же величины. Первый метод дает оценки 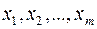этой величины, второй - 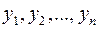. Требуется определить, обеспечивают ли оба метода одинаковую точность измерений.

2. Контроль точности работы некоторой производственной системы. Получаемые характеристики выпускаемой продукции характеризуются некоторым разбросом (дисперсией). Обычно величина этого разброса не должна превышать некоторого заранее заданного уровня. Требуется определить, обеспечивает ли система (например, линия сборки или отдельный станок) заданную точность.

Итак, статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой.

Наряду с выдвинутой гипотезой всегда рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то принимается противоречащая гипотеза.

Нулевой (основной) называют выдвинутую гипотезу .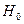

Альтернативной (конкурирующей) называют гипотезу 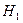, которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание нормального распределения равно 5, то альтернативная гипотеза, например, может состоять в предположении, что 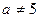. Кратко это записывают так: .

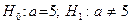Простой называют гипотезу, содержащую только одно предположение. Например, если 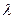- параметр показательного распределения, то гипотеза 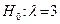- простая. Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза 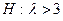состоит из бесконечного множества простых гипотез вида 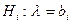, где 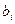- любое число, большее 3.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Так как проверку производят статистическими методами, то ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Следует отметить, что последствия ошибок могут оказаться различными. Если отвергнуто правильное решение "продолжать строительство жилого дома", то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение "продолжать строительство" несмотря на опасность обвала дома, то эта ошибка второго рода может привести к многочисленным жертвам. Иногда, наоборот, ошибка первого рода влечет более тяжелые последствия.

Естественно, правильное решение может быть принято также в двух случаях, когда принимается правильная гипотеза или отвергается неверная гипотеза.

Вероятность совершения ошибки первого рода называют уровнем значимости и обозначают 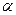. Чаще всего уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).

Дата добавления: 2014-01-06