Статистический критерий

Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно.

Статистическим критерием (или просто критерием) называют случайную величину (K), которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий .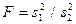

Очевидно, что эта величина случайная, т.к. в различных опытах исправленные дисперсии принимают различные, заранее неизвестные значения.

Наблюдаемым значением критерия K_набл называют значение критерия, вычисленное по выборкам. Например, если в вышеприведенном случае 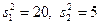, то K_набл = 20/5 = 4.

Критическая область. Область принятия гипотезы. Критические точки.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества, одно из которых содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Соответственно, о бластью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством 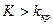, где 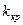- положительное число.

Левосторонней называют критическую область, определяемую неравенством 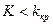, где 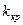- отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами 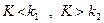, где 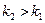. В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами 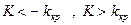или равносильным неравенством 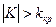. Различия между вариантами критических областей иллюстрирует следующий рисунок.

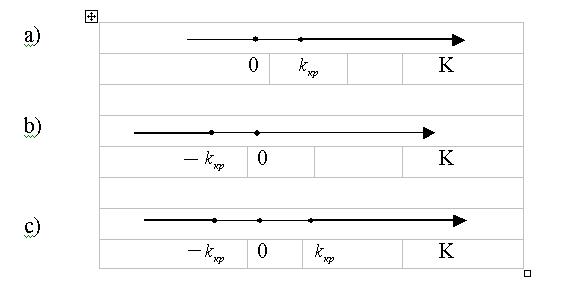
Рис. 1. Различные варианты критических областей a) правосторонняя, b) левосторонняя, с) двусторонняя

Мы подошли к вопросу об этапах проверки статистических гипотез.

Выделим следующие этапы:

· Формулируется нулевая гипотеза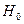

· Определяется критерий K, по значениям которого можно будет принять или отвергнуть 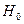и выбирается уровень значимости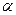

· По уровню значимости определяется критическая область

· По выборке вычисляется наблюдаемое значение критерия K, определяется, принадлежит ли оно критической области и на основании этого принимается гипотеза 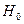или альтернативная гипотеза .

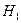Критерий согласия Пирсона о виде распределения.

Если закон распределения неизвестен, но есть основания предполагать, что он имеет определенный вид 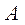, то проверяют нулевую гипотезу: генеральная совокупность распределена по закону 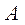. Проверка этой гипотезы производится при помощи специально подобранной случайной величины – критерия согласия.

Таким образом, к ритерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия, причем наиболее часто используемым является критерий согласия К. Пирсона ("хи квадрат").

Пусть по выборке объема 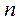получено эмпирическое распределение

Варианты……………………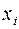
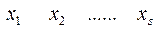
Эмпирические частоты…….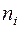

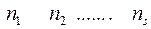
Для определенности рассмотрим сначала случай проверки статистической гипотезы о нормальном распределении генеральной совокупности.

Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты 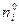. При уровне значимости 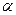требуется проверить нулевую гипотезу: генеральная совокупность распределе-на нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину

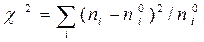(А)

Естественно, чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений.

Доказано, что при n ® ¥ закон распределения случайной величины (А) стремится к закону распределения 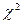с 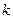степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия .

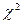Число степеней свободы определяется из равенства , где s – число групп (частичных интервалов) выборки, 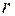– число параметров предполагаемого распределения. В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому число степеней свободы .

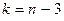Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости : .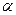

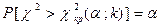Таким образом, правосторонняя критическая область определяется неравенством 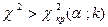, а область принятия нулевой гипотезы – соответственно неравенством 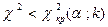. Обозначим значение критерия, вычисленного по данным наблюдений, через 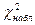и сформулируем правило проверки нулевой гипотезы:

Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H₀ : генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия 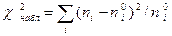и по таблице критических точек распределения 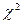, по заданному уровню значимости a и числу степеней свободы k = n – 3 найти критическую точку 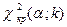. Если 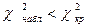- нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону.

Отметим два обстоятельства.

· Объем выборки должен быть достаточно велик (не менее 50). Каждая группа должна содержать не менее 5-8 вариант, а малочисленные группы следует объединять в одну, суммируя частоты.

· Поскольку возможны ошибки первого и второго рода, следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, построить предварительно график распределения и т.п.

Применение критерия согласия Пирсона не ограничивается случаем нормального распределения. Приведем примеры использования критерия Пирсона.

Пример1. При уровне значимости 0,05 проверить гипотезу о распределении по закону Пуассона генеральной совокупности, если по данным выборки объема 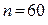получен следующий вариационный ряд:

Варианты	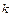	1	2	3	4	5	6	7
Частоты	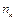8	17	16	10	6	2	0	1

Решение: Для расчета теоретических частот используем формулу Пуассона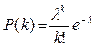

Для оценки параметра 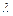используем соотношение

Вычислим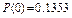

.

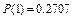
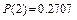
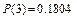
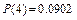
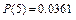
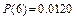
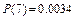Значение 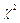равно .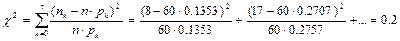

Вычислим число степеней свободы 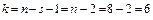. По таблице критических точек распределения хи-квадрат пр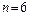и и 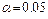находим 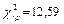. Так как наблюдаемое значение меньше критического, то наблюдаемые значения согласуются с распределением Пуассона и нулевая гипотеза принимается.

Пример 2. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты

Эмпирические частоты
Теоретические частоты

Рассчитаем 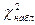= 7,19, число степеней свободы определим по соотношению k =s –3 = 5 (в нашем случае s = 8). Используя рассчитанные значения 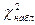и k, по таблице критических точек распределения хи-квадрат при уровне значимости 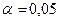находим 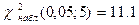. Так как 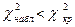, то нет оснований отвергать нулевую гипотезу. Данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Дата добавления: 2014-01-06