Плоскости симметрии

Плоскостью симметрии называется плоскость, которая делит фигуру на две равные части, расположенные друг относительно друга как предмет и его зеркальное отражение.

Плоскость симметрии обозначается буквой Р.

Симметрическое преобразование, отвечающее плоскости симметрии, есть отражение в плоскости.

Рис. 2.2. Фигура несимметричная

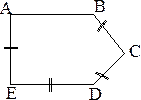
Для отражения некоторой фигуры АВD в плоскости Р (рис.2.3) из каждой её точки опускают перпендикуляры на плоскость отражения и продолжают их по другую сторону плоскости на расстояния, равные расстояниям отражаемых точек до плоскости Р. В результате получаем новую фигуру А₁В₁D₁.

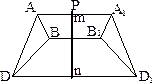
Рис. 2.3. Отражение точек фигуры в плоскости Р

При нахождении плоскостей симметрии мысленно рассекают их плоскостью на две половины так, чтобы при отражении в этой плоскости половинки совместились друг с другом.

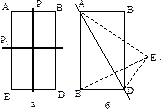
Не каждая плоскость, делящая фигуру пополам, является плоскостью симметрии. Например, в прямоугольнике только две плоскости параллельные его сторонам являются плоскостями симметрии (рис. 2.4). Плоскости идущие вдоль диагоналей прямоугольника плоскостями симметрии не являются, т. к. образующиеся треугольники зеркально не равны.

Рис.2.4. Прямоугольник АВDЕ имеет две плоскости (Р и Р₁) симметрии

Кристаллические многогранники могут иметь одну или несколько плоскостей симметрии. Число плоскостей симметрии указывается коэффициентом, стоящим перед буквой Р. Например, куб имеет 9Р, т. е. девять плоскостей симметрии (рис. 2.5).

Следует помнить, что плоскости симметрии или перпендикулярны к рёбрам и граням многогранника и проходят через их середины, или проходят вдоль рёбер.

Дата добавления: 2014-01-06