Стереографические проекции

Одной из характерных особенностей кристалла является постоянство углов между его гранями, а количество и размеры их могут меняться. Поэтому для изображения кристаллов применяют такие методы проектирования, которые дают точное представление о величине и расположении гранных углов. В этом отношении удобны стереографические проекции.

Примем некоторую точку О за центр проекции (рис.3.1). Произвольным радиусом опишем вокруг него шаровую поверхность, называемую шаром проекций. Через ту же точку проведём горизонтальную плоскость Q, которая принимается за плоскость проекций.

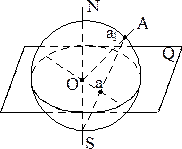
При пересечении шаровой поверхности с плоскостью проекций получаем большой круг, соответствующий экватору шара проекций и называемый кругом проекций.

Рис. 3.1. Построение стереографической проекции направления ОА

Вертикальный диаметр шара проекций NS, перпендикулярный к плоскости проекций, называется осью проекций. Точки пересечения сферической поверхности осью проекций NS являются точками зрения или полюсами шара проекций.

Рассмотрим получение стереографической проекции некоторого направления. Для этого перенесем его параллельно самому себе так, чтобы оно прошло через центр проекции.

Пусть после такого переноса направление заняло направление ОА. Точку пересечения направления ОА с шаровой поверхностью обозначим а₁. Соединим эту точку с нижней точкой зрения S лучом зрения Sa₁. Точка а, т. е. точка пересечения луча зрения с плоскостью проекции Q, является стереографической проекцией направления ОА.

Стереографические проекции направлений изображаются точками, лежащими в пределах круга проекций.

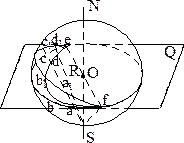
Рис. 3.2. Построение стереографической проекции плоскости R

Найдём теперь стереографическую проекцию некоторой плоскости R (рис. 3.2). Перенеся эту плоскость параллельно самой себе в центр проекций, продолжим её до пересечения с верхней полусферой шара проекций. В результате пересечения получаем на шаре дугу большого круга f a₁ b₁ c₁ d₁ e. Все точки этой дуги соединим лучами зрения с нижней точкой зрения. Проведённые лучи зрения в совокупности образуют так называемый проектирующий конус с вершиной в точке S.

Линия пересечения проектирующего конуса с плоскостью проекций представляет собой дугу окружности. Эта дуга является стереографической проекцией плоскости R.

Стереографические проекции плоскостей в общем виде изображают круговыми дугами.

Проектируя оси симметрии, необходимо продолжить их до пересечения со сферой, описанной произвольным радиусом вокруг кристалла из его центральной точки.

L_i6

L₆

L_i4

L₄

L₃

L₂

Рис.3.3. Обозначение осей симметрии на проекции

Пересечения осей с шаром проекций соединяются с нижней точкой зрения лучами.

Горизонтальные оси, совпадающие с плоскостью проекций, дают два выхода на круге проекций. Косо расположенные оси проектируются внутри круга проекций.

На стереографических проекциях оси симметрии обозначают значками, как показано на рис. 3.3. При проектировании плоскостей симметрии их продолжают до пересечения со сферой, на верхней половине которой получают дуги больших кругов.

Проекция вертикальной оси совпадает с центром круга проекций.

 

Если плоскость симметрии занимает вертикальное положение, то её стереографическая проекция изображается прямой линией, отвечающей одному из диаметров круга проекций (рис. 3.4).

Горизонтальная плоскость симметрии, совпадающая с плоскостью проекций, представляется кругом проекций, а проекция косо расположенная в плоскости симметрии отвечает круговой дуге (рис. 3.4).

Проекции плоскостей симметрии на чертежах принято изображать двойными линиями.

Перейдем далее к проектированию граней кристаллов.

Пусть нам задан некоторый кристаллический многогранник в виде прямой призмы. На рис. 3.5 основания этой призмы расположены перпендикулярно горизонтальной плоскости проекций Q, проходящей через центральную точку призмы О, из которой описана вокруг многогранника сферическая поверхность.

Чтобы спроектировать грань А, опускаем на неё перпендикуляр из центра проекций и продолжаем его до пересечения с поверхностью сферы. Точку а₁ этого пересечения соединяем лучом с нижним полюсом шара проекций. В результате пересечения луча зрения с плоскостью проекций получим точку а, которая является гномостереографической проекцией грани А.

Таким образом, проекцию грани кристалла получают как стереографическую проекцию нормали к ней и изображают точкой.

Описанным выше способом проектируем и остальные грани призмы. При этом перпендикуляры к вертикальным граням В и Е оказываются лежащими в плоскости проекций Q и поэтому они проектируются на сам круг проекций (точки b и e). Нормали к горизонтальным граням C и F совпадают с осью проекций NS, вследствие чего они проектируются в центре круга проекций (точки f и c).

Нормаль к нижней наклонной грани D пересекает шар проекций в нижней полусфере. При использовании нижней точки зрения проекция этой нормали выходит за пределы круга проекций. Неудобство такого построения вынуждает в подобных случаях переносить точку зрения в верхний полюс шара проекций N. Благодаря этому проекция нормали к грани D тоже попадает внутрь круга проекций (точка a).

Чтобы отличить на чертеже проекции нормалей к верхним и нижним граням, первые обозначают чистыми кружками, а вторые - крестиками.

Таким образом, из вышеприведённых построений следует, что горизонтальные грани проектируются всегда в центре круга проекций, вертикальные грани, на самом круге проекций, а косые грани внутри круга проекций.

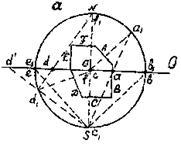
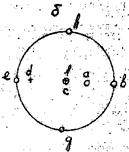
Рис. 3.5. Проектирование граней кристалла методом стереографических проекций (а); изображение проекций граней кристалла на плоскости проекции (б)

При этом, чем круче наклонена грань, тем ближе к кругу проекций располагается проектирующая её точка.

Если кристалл имеет центр инверсии, то около центра круга проекций ставится буква С.

Кристаллы кубической сингонии при проектировании принято ставить в положение при котором одна из этих осей совпадает с осью проекций. Две другие оси должны лежать в горизонтальной плоскости.

Кристаллы средней сингонии ориентируют так, чтобы главная ось симметрии располагалась вертикально.

Ромбические кристаллы ориентируют так, чтобы одна из осей второго порядка шла вертикально вверх, вторая на наблюдателя, третья слева направо.

Моноклинные и триклинные кристаллы ориентируют так, чтобы возможно большее количество их граней заняло вертикальное положение.

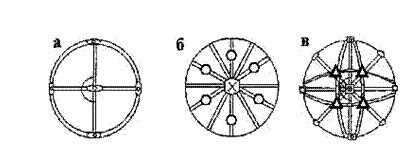В качестве примеров на рис. 3.6 приведены проекции элементов симметрии граней трёх многогранников различных категорий.

Рис. 3.6. Стереографические проекции элементов симметрии и граней: а – многогранника, имеющего форму прямоугольника, б – правильной шестиугольной пирамиды, в – куба

Дата добавления: 2014-01-06