Закон рациональности двойных отношений

УЧЕНИЕ О КРИСТАЛЛОГРАФИЧЕСКИХ СИМВОЛАХ

(закон Аюи)

Закон рациональности двойных отношений является важнейшим законом кристаллографии, из которого вытекает всё учение о кристаллографических символах, применяемых для определения относительного расположения граней и рёбер кристаллов. Закон этот был впервые сформулирован французским кристаллографом Аюи (1723-1826) и поэтому его часто называют “законом Аюи”. Сущность закона Аюи состоит в следующем.

Выберем в кристалле три непараллельных ребра, пересекающихся в одной точке (рис. 4.1). Пусть две непараллельные грани пересекают все три ребра первая грань в точках А₁,В₁,С₁, а вторая в точках А₂,В₂,С₂.

Таким образом грань А₁В₁С₁ отсекает на ребрах О₁,О₂,О₃ отрезки ОА₁, ОВ₁ и ОС₁, а грань А₂В₂С₂ - отрезки ОА₂, ОВ₂ и ОС₂.

Разделим отрезки отсекаемые на рёбрах одной гранью, на соответственные отрезки другой грани, а затем возьмём отношение трёх полученных дробей. В результате получим двойные отношения отрезков, которые можно заменить отношениями:

ОА₂/ ОА₁: ОB₂/ ОB₁: ОC₂/ ОC₁=m:n:p

где m,n,p- целые взаимно простые числа.

Это математическое выражение закона рациональности: “ Двойные отношения отрезков, отсекаемых двумя любыми гранями кристалла на трёх пересекающихся рёбрах его, равны отношениям целых и сравнительно небольших взаимно простых чисел ”.

Закон Аюи объясняется решётчатым строением кристаллов. Грани на рис. 4.1 соответствуют плоским сеткам, а рёбра рядам решётки.

Если а₀ – промежуток ряда О1, b₀-промежуток ряда О2, с₀-промежуток ряда О3 (рис. 4.2), то отрезки сетки A₁B₁C₁ равны:

ОА₁=rа₀, ОB₁=sb₀, ОC₁=t c₀,

где r,s,t- целые числа.

Отрезки сетки A₂B₂C₂ равны:

ОА₂=uа₀, ОB₂=vb₀, ОC₂=wc₀,

где u,v,w- целые числа.

Если плоские сетки проходят через узлы, которые располагаются вне рядов, то в этом случае отрезки, отсекаемые плоскими сетками, состоят из дробного, но обязательно рационального числа промежутков.

Рис. 4.1. Грани А₁В₁С₁ и А₂В₂С₂ отсекают на ребрах О1, О2, О3 отрезки, отношения которых равны отношениям простых чисел

Рис. 4.2. Ребра О1, О2, О3 - ряды решетки. Грани А₁В₁С₁ и А₂В₂С₂ - плоские сетки.

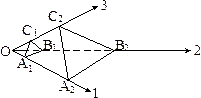
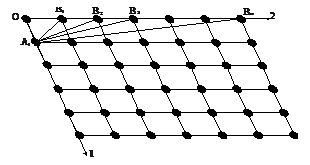
Рис. 4.3. Для действительных граней кристалла двойные отношения отрезков равны отношениям небольших целых чисел

В формулировке закона Аюи указывается, что двойные отношения отрезков равны отношениям сравнительно небольших целых чисел. Этот момент объясняется законом Бравэ.

Предположим, что два непараллельных ребра пересекаются различными гранями. Пусть все они отсекают на ребре отрезок, равный одному промежутку ряда. Прямые А₁В₁, А₁В₂ и т. д. отвечают следам всех этих граней на плоскости (рис. 4.3).

Пользуясь законом Аюи, можно теоретически вывести все возможные грани кристалла.

Дата добавления: 2014-01-06