Геометрическая интерпретация решения ЗЛП

Графический метод решения ЗЛП состоит из следующих этапов:

1. На координатной плоскости Х₁ОХ₂ строится область допустимых решений (ОДР). Она представляет собой многоугольник, стороны которого лежат на прямых, получаемых из системы ограничений задачи.
2. Строится вектор нормали q = (С₁,С₂) целевой функции (он указывает на направление возрастания целевой функции).
3. Строятся нижние и верхние опорные прямые, т.е. крайние линии уровня целевой функции, имеющие общие точки с ОДР. (Путем параллельного перемещения опорной прямой в направлении вектора нормали q).
4. Определяются координаты экстремальных точек и вычисляются значения целевой функции в них.

Пример 2.3

Решить графическим методом следующую задачу:

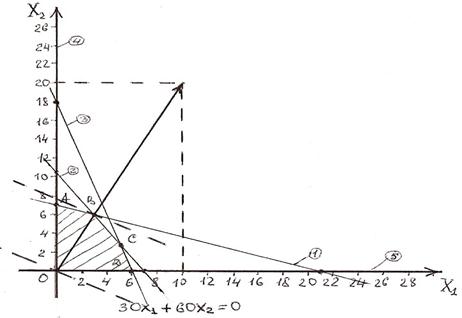
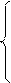х₁ + 3х₂ ≤ 21

3х₁ + 2х₂ ≤ 21

3х₁ + х₂ ≤ 18

х₁; х₂ ≥ 0

Определить при каких х₁ и х₂ функция F = 30х₁ +60х₂ → max

Решение.

1. Область допустимых решений построим следующим образом. Постоим прямые с уравнениями

Х1
Х2

1) х₁ + 3х₂ = 21

Х1
Х2	10,5

2) 3х₁ + 2х₂ = 21

Х1
Х2

3) 3х₁ + х₂ = 18

4) х₁ = 0

5) х₂ = 0

Прямые пронумерованы, а рядом с соответствующим уравнением приведены координаты двух точек, через которые проходят прямые.

В результате получим выпуклый пятиугольник ОАВСD.

2. Строим нормальный вектор q = (30;60)/ 3, уменьшив значение координат в 3 раза. Прямая с уравнением 30 х₁ + 60 х₂ = 0 представляет собой «нулевую» линию уровня целевой функции. Эта прямая проходит через начало координат и перпендикулярна нормальному вектору q. Передвигаем эту прямую параллельно себе по вектору q и фиксируем ее крайнее положение (т.В).

3. Определим координаты точки В, которая принадлежит прямым 1) и 2).

Составляется система уравнений:

х₁ + 3х₂ = 21 х₁ = 3; х₂ = 6

3х₁ + 2х₂ = 21

Тогда F _max =30∙3 + 60∙6 = 450

При минимизации F = 30 х₁ + 60 х₂ линию уровня необходимо смещать параллельно самой себе в направлении противоположном вектору q. Минимум функции достигается в точке О(0;0).

Тогда F _min = 0.

К достоинствам геометрического метода решения ЗЛП относятся:

- наглядность;

- быстрота и легкость нахождения ответа.

К недостаткам геометрического метода относятся:

- возможны «технические» погрешности при приближенном построении графиков;

- многие величины, имеющие четкий экономический смысл (остатки ресурсов производства, избыток питательных веществ и т.п.) не выявляются;

- этот метод легко применим, когда число переменных в стандартной задаче не превышает двух.

Дата добавления: 2014-01-06