Выполнить самостоятельно. В соответствии с заданием (табл

ЗАДАНИЕ №1.

В соответствии с заданием (табл. 1) решить задачу оптимизации графически. В задаче построить многоугольник допустимых решений. На многоугольнике определить точку выхода, определить координаты этой точки и значение целевой функции в точке выхода.

ТАБЛИЦА №1

	0,1,2	3,4,5,6	7,8,9
	f(x)=3x1-2x2; 2x1+x2≤2; x1+2x2≤2; x1,x2≥0;	f(x)=4x1+8x2; x1+x2≤3; x1+2x2≤2; x1,x2≥0;	f(x)=-4x1+8x2; 3x1+5x2≤15; x1-x3≤1; x1,x2≥0;
	f(x)=3x1-2x2; -x1+2x2≤2; 2x1-x2≤2; x1,x2≥0;	f(x)=-x1+6x2; 4x1+3x2≤12; -x1+x2≤1; x1,x2≥0;	f(x)=-x1+6x2; x1+x2≤3; -2x1+x2≤2; x1,x2≥0;
	f(x)=x1+6x2; 3x1+4x2≤12; -x1+x2≤2; x1,x2≥0;	f(x)=2x1+6x2; 3x1+4x2≤12; x1+2x2≤2; x1,x2≥0;	f(x)=8x1+12x2; 2x1+x2≤4; 2x1+5x2≤10; x1,x2≥0;
	f(x)=8x1+12x2; -3x1+2x2≤0; 4x1+3x2≤12; x1,x2≥0;	f(x)=3x1-2x2; 2x1+x2≤2; 2x1+3x2≤6; x1,x2≥0;	f(x)=6x1+4x2; x1+2x2≤2; -2x1+x2≤0; x1,x2≥0;
	f(x)=6x1+4x2; 3x1+2x2≤6; 3x1+x2≤3; x1,x2≥0;	f(x)=8x1+6x2; -x1+x2≤1; 3x1+2x2≤6; x1,x2≥0;	f(x)=8x1+6x2; -x1+x2≤2; 3x1+4x2≤12; x1,x2≥0;

2.5 Элементы линейной алгебры.

Любые m переменных системы уравнений с n переменными, где m < n называются основными (или базисными), если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n – m переменных называются неосновными (или свободными). Основными могут быть разные группы из n переменных. Максимальное число групп основных переменных равно числу сочетаний 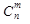(где m-число уравнений, а n-число переменных). Решение системы Х(х₁, х₂…х_n) называется допустимым, если оно содержит лишь неотрицательные компоненты, в противном случае решение называется недопустимым. Базисным решением системы m уравнений с n неизвестными называется решение в котором все (n – m) переменных равны 0. Допустимое базисное решение иначе называется опорным планом.

Пример 2.4.

Решить систему уравнений

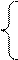х₁ – х₂ – 2х₃ + х₄ = 0

2 х₁ + х₂ + 2х₃ – х₄ = 2

Общее число групп основных переменных: 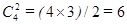- X₁X₂, X₁X₃, X₁X₄, X₂X₃, X₂X₄, X₃X₄.

Выясним, могут ли быть основными переменные X₁X₂ , т.к. определитель матрицы из коэффициентов

׀ 1 -1 ׀ = 1•1 – 2•(-1) ≠ 0,

׀ 2 1 ׀

то X₁X₂ – основные переменные

Аналогично основным можно отнести X₁X₃; X₁X₄ (у них определители ≠ 0)

Группы X₂X₃, X₂X₄, X₃X₄ не могут быть основными, т.к. их определители = 0

Таким образом система уравнений имеет 3 базисных решения:

1) Для основных переменных X₁X₂ и не основных X₃X₄

(X₃= X₄ = 0)

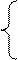
Х₁-Х₂=0 X₁ = ⅔

2Х₁+Х₂=2 X₂ = ⅔

Таким образом, базисное решение: X = (⅔, ⅔, 0, 0) – допустимое решение;

2) Для основных переменных X₁X₃ и неосновных X₂ = X₄ = 0

X₁ = ⅔ X₃ = ⅓

Базисное решение: X₂ = (⅔, 0, ⅓, 0). Оно тоже допустимое.

3) Для основных переменных X₁ X₄ и неосновных X₂ = X₃ = 0

Базисное решение X₃ (⅔, 0, 0, -⅔) – недопустимое.

2.6 Симплекс-метод (СМ) решения ЗЛП

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины к соседней, в которых целевая функция принимает лучшие значении до оптимального значения.

В настоящее время СМ используется для компьютерных расчетов, однако не сложные методы можно решать и вручную.

Для реализации СМ необходимо знать 3 основных элемента:

1. способ определения первоначального допустимого базисного решения;

2. правило перехода к лучшему решению;

3. проверка признака оптимальности решении, который состоит в следующем:

- если в выражении целевой функции отсутствуют положительные коэффициенты при неосновных переменных, то решение максимально;

- если отсутствуют отрицательные коэффициенты, то решение минимально.

Для нахождения первоначального базисного решения разобьем переменные на две группы – основные и не основные. При выборе основных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и проверять, равен ли он 0.

Достаточно ввести дополнительные неотрицательные переменные с учетом правила определения знака дополнительных переменных:

Знак «+», если неравенство вида ≤;

Знак «-», если неравенство вида ≥.

Дата добавления: 2014-01-06