Методы определения локального экстремума функции нескольких переменных

а) Метод Гаусса – Зейделя

Метод поочередного изменения параметров (переменных), или метод покоординатного спуска (подъема).

Суть метода: поочередная оптимизация последовательно по каждой переменной.

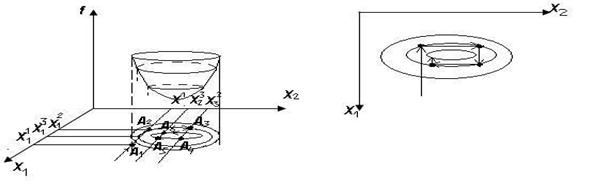
Обрабатывается функция n переменных. По каждой переменной задана область изменения. Случайным образом выбирается т. А₁.

А₁:х₁^′,х₂^′, х₃′,…, х_n′ => f( х₁^′,х₂^′ , х₃′,…, х_n′ )

⁼

х₁ рассматривается в целевой функции, а другие переменные фиксируются. Применяется один из рассмотренных ранее методов. Затем находится т.А_2.

А₁:х₁²,х₂^′, х₃′,…, х_n′ => f( х₁², х₂^′ , х₃′,…, х_n′ )

⁼

Берется следующая переменная – х₂. Целевую функцию рассматриваем как функцию переменной х₂,остальные переменные фиксируются. Используем один из методов для функции одной переменной и получаем т. А₃.

А₃=:х₁²,х₂², х₃′,…, х_n′ и т.д. процесс повторяется.

Характерные черты метода: Спираль выбранных точек имеет прямые углы. Метод обеспечивает поиск только локального экстремума. Результаты анализа целевой функции зависят от первоначально выбранной точки.

Преимущество: простота алгоритмизации. Алгоритм останавливается, когда разница между значениями целевой функции достаточно мала (она задается).

б) Метод градиента(наиболее распространен)

Суть метода: нахождение направления движения, в котором целевая функция наибольшим образом изменяется и осуществление следующего шага в этом направлении.

Градиент функции – вектор, который характеризует направление наибольшего возрастания функции.

Антиградиент – уменьшение функции. grad f^N (х¹,х²,...,хⁿ)=(∂ f^N/ ∂ х¹_, ∂ f^N/ ∂ х²_,..., ∂ f^N/ ∂ хⁿ), вычисленный в точке N

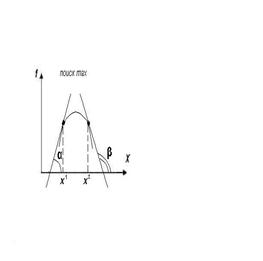
∂ f^N/ ∂ х¹ = tgα > 0(≤α < 90 ^*) - значит ∂ f^N/ ∂ х¹ = tgα <0 - значит нужно шагать вправо(увеличивать х). нужно шагать вправо(увеличивать х).

∂ f^N/ ∂ х² = tgβ< 0(≤α > 90 ^*) - ∂ f^N/ ∂ х² = tgβ> 0 - значит нужно шагать влево.

значит нужно шагать влево (уменьшать х).

(уменьшить х).

Для max следующая точка х^N+1 = x^N+ (∂ f^N/ ∂ хⁿ) ∙ h

h- вспомогательная величина.

Если ∂ f^N/ ∂ хⁿ =0, то в этой точке экстремум.

Для min следующая точка х^N+1 = x^N- (∂ f^N/ ∂ хⁿ) ∙ h

В случае n- мерного пространства:

_

х_i ^N+1=x_i^N+(∂ f^N/ ∂х_iⁿ)∙h; i=1,n – max

_ (1)

х_i ^N+1 = x_i^N - (∂ f^N/ ∂ х_i ⁿ) ∙ h; i=1, n - min

Дата добавления: 2014-01-06