Обоснование вида функции энтропии

Количество информации I можно оценить величиной неопределенности, устраняемой в результате принятия сообщения.

Пусть существует объект L, о котором в настоящий момент времени получатель не имеет сведений. Тогда его неопределенность H(L) равна полному незнанию об источнике данных. С получением сообщения a часть неопределенности об источнике сообщения снята, но какое-то незнание осталось – Ha (L). Тогда количество информации в сообщении можно измерить как разность между неопределенностью об источнике до сообщения и неопределенностью, оставшейся после получения сообщения:

I (L) = H (L) – Ha (L).

Мера неопределенности об источнике сообщений получила название энтропия.

Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

Для практики важно иметь возможность произвести численную оценку энтропии разных опытов.

Пусть опыт имеет n равновероятных исходов. Исходы равновероятны, если ни одно из них не имеет преимущества перед другими. Очевидно, что энтропия данного опыта зависит от величины n, т.е. является функцией числа возможных равновероятных исходов f (n):

1. f (1) = 0, поскольку возможный исход не является случайным;

2. f (n) возрастает с ростом числа возможных исходов n, поскольку чем больше число возможных исходов, тем трудней предугадать результат опыта.

Пусть проводятся два (или больше) независимых опыта a и b с количествами равновероятных исходов в каждом соответственно na и nb. Очевидно, мера суммарной неопределенности опытов a ^ b равна сумме неопределенностей:

3. f (na * nb) = f (na) + f (nb) – свойство аддитивности.

Таким образом, энтропия должна описываться функцией, обладающей тремя необходимыми свойствами – 1,2,3. Такому набору свойств соответствует лишь логарифмическая функция, причем ее основание не имеет значения (loga x = logb x * loga b). На практике выбирают основание 2, так как это оказывается удобным при принятии единицы информации бит - при n = 2 равновероятных исходах log2 n = 1 бит. Энтропия опыта с n равновероятными исходами – H (a) = log 2 (n).

Энтропия одного исхода в опыте с возможными n равновероятными исходами:

H = (1/ n) * log 2 (n) = -(1/n) * log 2 (1/n) = - p*log2 p,

где p = 1/n – вероятность любого из отдельных исходов.

Таким образом, энтропия каждого возможного исхода равна

H = - p*log2 n.

Обобщая это выражение на опыт с n не равновероятными исходами A1…An получим:

H (a) = -∑ p (Ai) * log2 p (Ai).

Энтропия обладает рядом свойств:

H (a) – вещественная и неотрицательная величина (знак минус учитывает, что значение величины под логарифмом меньше единицы, т.е. 0 < pi < 1 дробное).

1. Энтропия не учитывает содержательную сторону информации, т.е. ее ценность.

2. Энтропия нескольких независимых источников сообщений равна сумме энтропии каждого из них: H (a*b) = H (a) + H (b).

3. Энтропия – величина ограниченная. При прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.

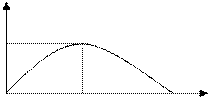H

p

0, 5

Энтропия опыта равна той информации, которую получаем в результате его осуществления, т.е. I = H(a) – информация опыта равна среднему количеству информации одного его исхода.

I = –∑ p (Ai) * log2 p (Ai).

Для случая, когда все n исходы равновероятны p (Ai) = 1 / n и

I = –∑ p (Ai) * log2 p (Ai) = –∑ (1/n) * log2 (1/n) = ∑ (1/n) * log2 (n) = log2 (n)

Таким образом, в случае равновероятных исходов по формуле Р. Хартли количество информации определяется числом возможных исходов. Данная формула связывает количество равновероятных состояний (n) и количество информации в сообщении (I), что любое из этих состояний реализовалось. Ее смысл в том, что, если некоторое множество содержит n элементов и x принадлежит данному множеству, то для его выделения (однозначной идентификации) среди прочих требуется количество информации, равное log2 (n).

Алфавитный (кибернетический) подход – это единственный способ измерения информации, циркулирующей в информационной технике (компьютерах). Здесь речь идет об измерении информации в тексте (символьном сообщении), составленном из символов некоторого алфавита. К содержанию текста (семантике сообщения) такая мера информации отношения не имеет. Поэтому такой подход можно назвать объективным, т.е. не зависящим от воспринимающего его субъекта.

Базовым понятием в данном подходе является понятие алфавита. Алфавит – это конечное множество символов, используемых для представления информации. Число символов в алфавите называется мощностью алфавита. В предположении, что вероятности появления каждого символа алфавита одинаковы (что на практике далеко не так), количество информации, которое несет в тексте каждый символ (i) вычисляется из уравнения Хартли: 2 ^ i = N, где N – мощность алфавита. Величину (i) можно назвать информационным весом символа. Отсюда следует, что количество информации во всем тексте, состоящим из K символов, равно произведению информационного веса символа на их количество:

I = i * K.

Величина I - информационный объем текста. Поэтому данный подход носит название объемного подхода.

Минимальная мощность алфавита, пригодного для передачи информации, равна 2. Такой алфавит называют двоичным. Информационный вес символа в двоичном алфавите: поскольку 2 ^ i = 2, то i = 1. Эта величина получила название бит. Один символ двоичного алфавита несет 1 бит информации.

Бит – основная единица измерения информации. Существуют и производные единицы измерения: 1 байт = 8 бит (256 = 2 ^8 – мощность алфавита ПК); 1 килобайт = 1024 байта, т.е больше 1 байта в 2^10 раз; 1 мегабайт = 1024 килобайта.

Говоря о символьном сообщении как последовательности знаков определенного алфавита и считая вероятность появления каждого отдельного знака неизменной во времени (шенноновское сообщение) можно определить среднее количество информации одного знака в сообщении.

Если за исходное положение принять равную вероятность появления каждого знака в сообщении, то количество информации, приходящееся на один знак алфавита, находим по формуле Хартли:

I0 = log2 (n).

Для английского алфавита I = log2 (n) = log2 27 = 4,755 бит, а для русского алфавита I = log2 (n) = log2 34 = 5,087 бит.

Определим среднее количество информации, приходящейся на один знак, если вероятности появления различных букв алфавита в сообщении не одинаковы:

I1 = –∑ p i * log2 p i.

Эту формулу открыл К. Шеннон, с работы которого (1948) принято начинать отсчет возраста информатики, как самостоятельной науки.

Следующим приближением при оценке значения информации, приходящейся на один знак алфавита, должен быть учет корреляции, т.е. связей между буквами в словах. Значение I∞, полученное после учета бесконечного числа корреляций между буквами данного алфавита в словах, является предельным значением количества информации на один знак данного алфавита, отражающей минимальную неопределенность выбора знака алфавита без учета семантических особенностей языка.

Относительная избыточность языка R = 1 – (I∞ / I0) показывает долю лишней информации текстов данного языка. Лишней в том отношении, что эта доля определяется структурой самого языка и может быть восстановлена в сообщении без явного выражения в буквенном виде.

Дата добавления: 2014-01-06