Временные булевы функции

Кроме комбинационных схем, называемых схемами первого рода, различают, как упоминалось выше, накапливающие схемы, включающие элементы с памятью. Основной особенностью схем с памятью является тот факт, что алгоритм их работы зависит от времени. Поэтому в число переменных для функций, описывающих накапливающие схемы, должно входить время t. Однако время не является двоичной переменной. Поэтому вводится так называемое автоматное время, принимающее дискретные целочисленные значения 0, 1, 2,..., и т.д. Это означает, что работа схемы с памятью распадается на ряд интервалов, в течение которых автоматное время условно принимает постоянное значение.

Определение. Временная булева функция (ВБФ) это логическая функция y=φ(х₁,х₂,...,х_n,t), принимающая значение {0,1} при 0≤t≤s-1, где s‑ количество интервалов автоматного времени:

0 1 s‑1

│ ││ │ │ │ │ │ t

0 1 2... s‑1 s

Существует теорема о том, что любая периодическая временная булева функция может быть представлена в аналитическом виде следующим образом:

y = φ(х₁,х₂,...,х_n,t) = φ₀τ₀ + φ₁τ₁ +... + φ_s-1τ_s-1,

где φ _i- конъюнктивный терм (или их дизъюнкция) от переменных х₁,х₂,,...,х_n; τ_i- вспомогательная функция, принимающая значение из множества {0,1} в момент времени t_i.

Такая форма представления временных логических функций позволяет применить к функциям» все методы упрощения и минимизации ФАЛ.

Пример: преобразовать функцию, представленную таблицей, в аналитический вид.

х1	х2	t	φ(х1, х2, t)

Решение. Функция определена на трёх интервалах времени и поэтому представляем её совокупностью трёх логических функций φ ₀(x₁,x₂,t), φ ₁(x₁,x₂,t) и φ₂(x₁,x₂,t), которые для значений функции, равных 1, могут быть представлены следующим образом

φ ₀(x₁, x₂, t) = х_1`х₂, для t = 0;

φ ₁(x₁, x₂, t) = `х<sub>1</sub> х<sub>2</sub> + х<sub>1`</sub>х₂, для t = 1;

φ ₂(x₁, x₂, t)= x_1`x₂+ x₁ x₂ = x₁, для t = 2.

Определяем значение временного параметра ВБФ для каждого временного интервала:

для t = 0 – только τ₀ = 1;

для t = 1 - только τ₁ = 1;

для t = 2 – только τ₂ = 1;

Следовательно, аналитическое выражение таблично заданной ВБФ:

y = x<sub>1`</sub>x<sub>2</sub> τ<sub>0</sub>+ (`x₁x₂+ x_1`x₂) τ₁+ x₁τ₂.

Схема для полученной формулы строится аналогично с построением комбинационных схем плюс элемент-дешифратор, имеющий вид:

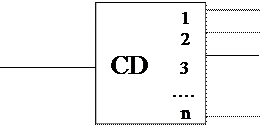t0

t1

t2

tn

где τ _i - выход i‑й функции, принимающей значение, равное 1 в t_i; все остальные τ в данный момент равны 0.

Если ВБФ зависит ещё и от своих предшествующих значений, то она называется рекуррентной булевой функцией (РБФ):

Y = φ[x₁(t), x₂(t),..., x_n(t),y(t‑1),y(t‑2),...,y(t‑k)],

где х_i (t)- текущее значение i‑й переменной; y(t‑k)- значение функции в момент времени t‑k.

Если, например, для функции y справедливо соотношение y(t+1)=x(t), то это означает, что значение выходного сигнала схемы в момент времени t+1 равен значению входного сигнала в момент времени t. Таким образом, схема выдаёт значение входа с задержкой на один интервал времени. Если такое соотношение справедливо для всех моментов времени, на которых определена функция y, то соответствующая ей схема называется элементом (схемой) задержки. Логический оператор, соответствующий элементу задержки, обозначается следующим образом

x(t) x(t‑1)

Любая РБФ может быть реализована с помощью набора логических операторов, представляющих обычные функции алгебры логики и операторов схем задержки.

Пример.

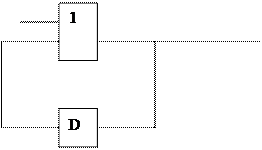x(t)

f=(x(t) + x(t-1))

x(t-1)

Дата добавления: 2014-01-06