Граф и график соответствия. Соответствие, обратное данному. Виды соответствий

Понятие соответствия. Способы задания соответствий

СООТВЕТСТВИЯ МЕЖДУ ДВУМЯ МНОЖЕСТВАМИ

Лекция 16. Соответствия

План:

1. Понятие соответствия. Способы задания соответствий.

2. Граф и график соответствия. Соответствие, обратное данному. Виды соответствий.

3. Взаимно-однозначные соответствия

Первоначально алгеброй называли учение о решении уравнений. За много столетий своего развития алгебра превратилась в науку, которая изучает операции и отношения на различных множествах. Поэтому не случайно уже в начальной школе дети знакомятся с таки­ми алгебраическими понятиями, как выражение (числовое и с пере­менными), числовое равенство, числовое неравенство, уравнение. Они изучают различные свойства арифметических действий над числами, которые позволяют рационально выполнять вычисления. И конечно, в начальном курсе математики происходит их знакомство с различ­ными зависимостями, отношениями, но чтобы использовать их в це­лях развития мыслительной деятельности детей, учитель должен овла­деть некоторыми общими понятиями современной алгебры - поняти­ем соответствия, отношения, алгебраической операции и др. Кроме того, усваивая математический язык, используемый в алгебре, учитель сможет глубже понять сущность математического моделирования реальных явлений и процессов.

Изучая окружающий нас мир, математика рассматривает не только его объекты, но и главным образом связи между ними. Эти связи называют зависимостями, соответствиями, отношениями, функциями. Например, при вычислении длин предметов устанавливаются соответствия между предметами и числами, которые являются значениями их длин; при решении задач на движение устанавливается зависимость между пройденным расстоянием и временем, если скорость движения постоянна.

Конкретные зависимости, соответствия, отношения между объектами в математике изучались с момента ее возникновения. Но вопрос о том, что общее имеют самые разные соответствия, какова сущность любого соответствия, был поставлен в конце XIX - начале XX века, и ответ на него был найден в рамках теории множеств.

В начальном курсе математики изучаются различные взаимосвязи между элементами одного, двух и более множеств. Поэтому учителю надо понимать их суть, что поможет ему обеспечить единство в методике изучения этих взаимосвязей.

Рассмотрим три примера соответствий, изучаемых в начальном курсе математики.

I. Найти значение выражения:	II.Найти площадь фигуры	III. Решить уравнение:
в1) (17-1):4; в2) (12 + 18): (6-6); в3) 2·7 + 6.	F1 F2 F1 Рис.66	y1) 2 + x = 6; y2) x – 7 = 4; y3) 2 x = 8

В первом случае мы устанавливаем соответствие между заданными выражениями и их числовыми значениями. Во втором выясняем, какое число соответствует каждой из данных фигур, характеризуя ее площадь. В третьем ищем число, которое является решением уравнения.

Что общее имеют эти соответствия?

Видим, что во всех случаях мы имеем два множества: в первом -это множество из трех числовых выражений и множество N натуральных чисел (ему принадлежат значения данных выражений); во втором -это множество из трех геометрических фигур и множество N натуральных чисел; в третьем - это множество из трех уравнений и множество N натуральных чисел.

Выполняя предложенные задания, мы устанавливаем связь (соответствие) между этими множествами. Ее можно представить наглядно, при помощи графов (рис. 67).

Можно задать эти соответствия, перечислив все пары элементов, плодящихся в заданном соответствии:

I. {(в₁,4),(в₃,20)};

II. {(F₁,4),(F₂,10),(F₃,10)};

III. {(y₁, 4), (у₂, 11), (y₃,4)}.

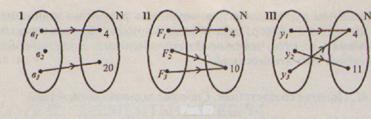
Рис. 67

Полученные множества показывают, что любое соответствие меж­ду двумя множествами X и Y можно рассматривать как множество упорядоченных пар, образованных из их элементов. А так как упоря­доченные пары - это элементы декартова произведения, то приходим к следующему определению общего понятия соответствия.

Определение. Соответствием между множествами X и Y назы­вается всякое подмножество декартова произведения этих мно­жеств.

Соответствия принято обозначать буквами Р, S, Т, К и др. Если S -соответствие между элементами множеств X и Y то, согласно опреде­лению, S с Х х У.

Выясним теперь, как задают соответствия между двумя множест­вами. Поскольку соответствие - это подмножество, то его можно за­давать как любое множество, т.е. либо перечислив все пары элементов, находящихся в заданном соответствии, либо указав характеристиче­ское свойство элементов этого подмножества. Так, соответствие меж­ду множествами X - {1, 2, 4, 6} и У = {3, 5} можно задать:

1) при помощи предложения с двумя переменными: а < Ь при условии, что а € X, b € Y;

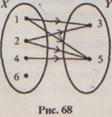
2) 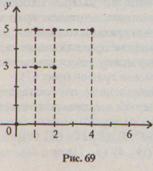перечислив пары чисел, принадлежащих подмножеству декартова произведения Х х У: {(1,3), (1,5), (2, 3), (2, 5), (4, 5)}. К этому спосо­бу задания относят также задание соответствия при помощи графа (рис. 68) и графика (рис. 69).

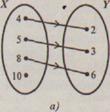
Нередко, изучая соответствие между множествами X и Y, приходится рассматривать и соответствие, ему обратное. Пусть, например, S -соответствие «больше на 2» между множествами X = {4, 5, 8, 10} и Y = {2, 3,6}. Тогда S = {(4,2), (5, 3), (8,6)} и его граф будет таким, как на рисунке 70,а.

Соответствие, обратное данному, - это соответствие «меньше на 2», Оно рассматривается между множествами R и Х, и чтобы его предста­вить наглядно, достаточно на графе соответствия S направление стрелок поменять на противоположное (рис. 70,6). Если соответствие меньше на 2» обозначить S^-1, то S^-1 = {(2,4), (3,5), (6,8)}.

Рис.70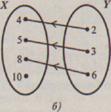

Условимся предложение «элемент х находится в соответствии S с элементом у» записывать кратко так: хSу. Запись хSу можно рас­сматривать как обобщение записей конкретных соответствий: x = 2у; х > 3у+1 и др.

Дата добавления: 2014-01-06