Лекция 10. Качественные характеристики зубчатой передачи

Качественные характеристики зубчатой передачи.

Коэффициент перекрытия

Рассмотрим процесс зацепления зуба шестерни с зубом колеса. В т. a вершина колеса касается ножки зуба шестерни. В т. b вершина того же зуба шестерни выходит из зацепления с ножкой зуба колеса (рис. 30).

При этом шестерня поворачивается на угол φ_γ, который называется углом перекрытия.

Коэффициентом перекрытия ε называется отношение угла перекрытия к угловому шагу τ.

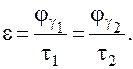
Угол φ_γ соответствует дуге d₁d₂ основной окружности, которая по построению эвольвенты равна длине практической линии зацепления ab.

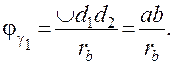
Угловой шаг – это центральный угол между осями симметрий соседних зубьев

,

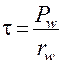где P_w – шаг зацепления по начальной окружности

r_w – радиус начальной окружности

Таким образом, торцовый коэффициент перекрытия (на рис. 30 представлено торцевое сечение передачи) вычисляется так:

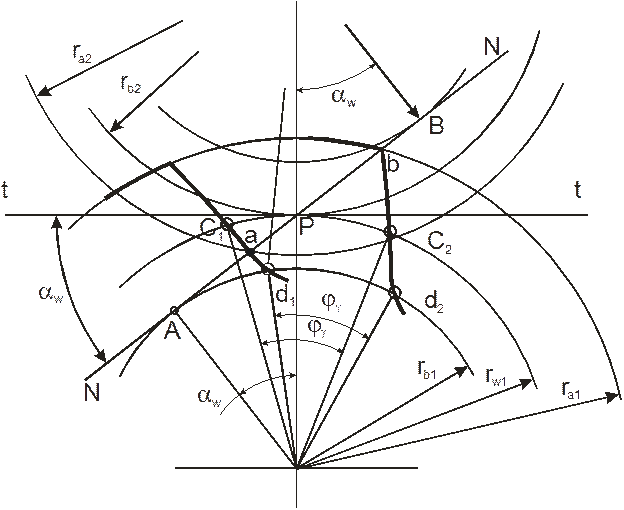
Рис. 30

Из геометрии зубчатого зацепления (рис. 30) следует:

,

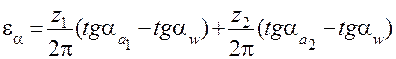где 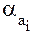– углы при вершинах зубьев шестерни () и колеса ().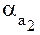

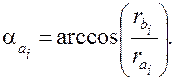
Коэффициент торцового перекрытия в прямозубой передаче должен быть больше 1,0, т.к. в противном случае, когда одна пара зубьев выйдет из зацепления, другая пара ещё не войдёт в зацепление и произойдет перерыв в контакте зубьев, сопровождаемый ударным приложением усилия в зацеплении.

Для косозубых зацеплений, зубья которых входят в контакт не одновременно всей боковой поверхностью, как прямозубые, а постепенно, рассматривается суммарный коэффициент перекрытия.

,

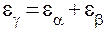где 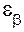– коэффициент осевого перекрытия

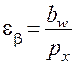
где p_x – осевой шаг

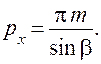
Для косозубых и шевронных колес торцовый коэффициент перекрытия ε_α может быть меньше 1,0.

Скорость скольжения зубьев. Коэффициент удельного скольжения.

Рассматриваемые характеристики необходимы при расчете зубьев на износостойкость, а также при оценке затрат мощности на трение.

Рассмотрим относительное и абсолютное движение т. K контакта боковых поверхностей зубьев шестерни и колеса (рис. 31).

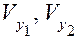– абсолютные скорости т. K.

По основному закону зацепления проекции векторов этих скоростей на линию зацепления должны быть равны.

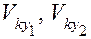– проекции векторов 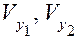на касательную к боковым поверхностям зубьев (перпендикуляр к линии зацепления).

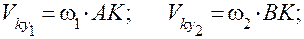
где 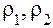– радиусы кривизны эвольвент боковых поверхностей зубьев в точке контакта K.

Скорости скольжения профилей зубьев

.

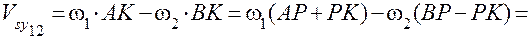
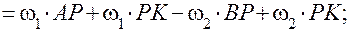
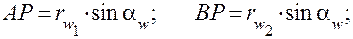
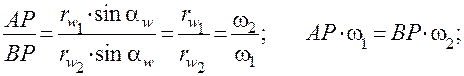
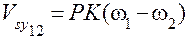На основании полученной зависимости можно построить график (рис.32) и определить значения скорости скольжения в любой точке практической линии зацепления ab.

Коэффициенты удельного скольжения:

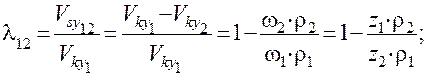
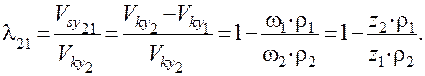
В полюсе зацепления P (рис. 31):

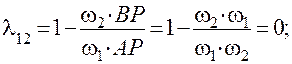
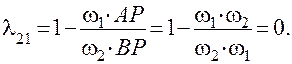
В т. A ρ₁=0, λ ₁₂ =−∞; λ ₂₁ =1,0

В т. B ρ₂=0, λ ₁₂=1,0; λ ₂₁=−∞

В остальных точках линии зацепления значения ν ₁₂ и ν ₂₁ можно определить, измерив радиусы кривизны ρ₁ и ρ₂.

По результатам расчетов строится графическая зависимость (рис. 33).

Рис. 31

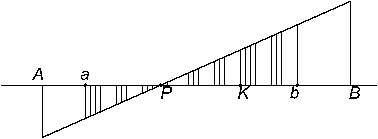
Рис. 32

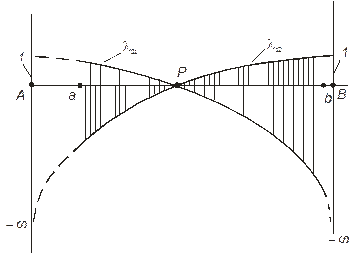
Рис. 33

Библиографический список.

1. Артоболевский.И.И. Теория механизмов и машин/ И.И..Артоболевский. М.: Наука, 1988.

2. Юдин.В.А Теория механизмов и машин/ В.А. Юдин, Л.В. Петрокас. М.: Высшая школа, 1977.

3. Соколовкий_В.И. Кинематический анализ и синтез механизмов/ В.И..Соколовский. Свердловск, УПИ 1979.

4. Соколовкий_В.И Динамический анализ и синтез механизмов/ В.И..Соколовский. Свердловск, УПИ 1979.

5. Попов_С.А. Курсовое проектирование по теории механизмов и механике машин/ С.А. Попов. М.: Высшая школа, 1986.

6. Теория механизмов и машин. Проектирование/ под редакцией Кульбачного О.И. М.: Высшая школа, 1970.

7. Крайнев_А.Ф. Словарь_–_справочник по механизмам/ А.Ф._Крайнев._ М.:_Машиностроение, 1987.

Учебное издание

Владимир Борисович Покровский

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН. ДИНАМИЧЕСКИЙ АНАЛИЗ. ЗУБЧАТЫЕ ЗАЦЕПЛЕНИЯ

Корректор Н.П. Кубыщенко

Компьютерная верстка: А.А. Кухтина, К.А. Бабхановского

Подписано в печать 25.11.2004 Формат 60×84 1/16 Бумага типографическая Офсетная печать Усл. печ. л. 2,91 Уч.-изд. 2,2 Тираж Заказ Цена “C”

ООО «Издательство УМЦ УПИ»

620002, Екатеринбург, ул. Мира, 17.

Дата добавления: 2014-01-06