Спрос потребителя в неопределенности. Существование функции ожидаемой полезности

Неопределенность - это жизненный факт. Каждый раз, принимая душ, переходя улицу или делая инвестиции, люди сталкиваются с различного рода рисками. Существуют, однако, финансовые институты, такие, как рынки страховых услуг и фондовый рынок, которые способны смягчать, по крайней мере, некоторые из этих рисков. Для понимания функционирования этих рынков необходимо изучить индивидуальное поведение в отношении выбора в условиях неопределенности.

Потребителя, по-видимому, интересует распределение вероятностей получения различных потребительских товарных наборов. Распределение вероятностей состоит из перечня различных исходов - в данном случае, потребительских наборов - и вероятностей, связанных с каждым исходом. Принимая решение о том, на какую сумму застраховать автомобиль или какие инвестиции произвести на фондовом рынке, потребитель фактически выбирает структуру распределения вероятностей получения различных величин потребления.

Если предпочтения потребителя в отношении потребления при различных обстоятельствах разумны, то можно использовать для описания этих предпочтений функцию полезности, подобно тому, как это делалось нами в другом контексте. Однако, тот факт, что мы рассматриваем выбор в условиях неопределенности, все же порождает особую структуру задачи выбора. Вообще, то, как потребитель оценивает потребление при одном исходе по сравнению с потреблением при другом исходе, зависит от вероятности того, что рассматриваемый исход действительно будет иметь место. Другими словами, пропорция, в которой я готов заместить потребление в случае дождя потреблением в случае отсутствия дождя, должна быть как-то связана с тем, насколько вероятным я считаю то, что дождь пойдет. Предпочтения в отношении потребления при разных состояниях природы зависят от предположений индивида в отношении того, насколько вероятно наступление этих состояний.

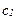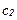По этой причине, мы можем представить функцию полезности зависщей не только от уровней потребления, но и от вероятностей. Предположим, что мы рассматриваем два взаимоисключающих состояния, таких, как дождь и ясная погода, потеря или ее отсутствие, или еще какие-то состояния. Обозначим через и потребление в состояниях 1 и 2, а через 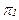и - вероятности того, что эти состояния будут иметь место в действительности. Если два рассматриваемых состояния взаимоисключающи, так что реально может наступить только одно из них, то 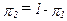. Но обычно мы выписываем обе вероятности, просто чтобы запись выглядела симметричной.

С учетом сделанных обозначений, можно записать функцию полезности для потребления в состояниях 1 и 2 в виде 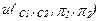. Это - функция полезности, представляющая предпочтения, имеющиеся у индивида в отношении потребления в каждом из состояний. Практически любые из примеров функций полезности, с которыми мы до сих пор имели дело, могут быть рассмотрены с позиций выбора в условиях неопределенности. Один из удачных примеров такого рода - случай совершенных субститутов. В этом случае взвешивание каждой величины потребления вероятностью того, что это потребление будет иметь место, представляется вполне естественным. Это дает нам функцию полезности вида .

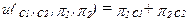При анализе выбора в условиях неопределенности выражение такого рода именуют ожидаемым значением. Это - не что иное, как средний уровень потребления, который был бы вами достигнут в итоге.

Другой пример функции полезности, которую можно использовать для изучения выбора в условиях неопределенности, - функция полезности Кобба-Дугласа: .

В этом случае полезность, приписываемая любой комбинации потребительских наборов, зависит от структуры потребления нелинейным образом. Как обычно, можно провести монотонное преобразование функции полезности, получив в результате него функцию, представляющую те же самые предпочтения. Оказывается, логарифм функции Кобба-Дугласа очень удобен для дальнейшего нашего анализа. Это дает нам функцию полезности вида .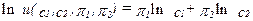

Ожидаемая полезность

Одной из особенно удобных форм, которую может принимать функция полезности, является следующая: 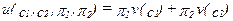. Она говорит нам о том, что функция полезности может быть представлена в виде взвешенной суммы неких функций потребления в каждом состояни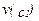и, и 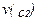, причем соответствующие веса заданы вероятностям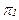и и .

Два примера этого рода приведены выше. В этой форме, при v(c)=c, была приведена функция полезности для совершенных субститутов, записанная как ожидаемое значение функции полезности. Функция полезности Кобба-Дугласа первоначально была приведена не в этой форме, но, когда мы выразили ее через логарифмы, она приняла линейную форму с .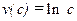

Если одно из состояний обязательно наступит, так что, скажем,, то 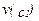есть полезность определенного потребления в состоянии 1. Аналогичным образом, если 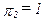, то 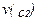есть функция потребления в состоянии 2. Таким образом, выражение 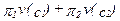представляет собой среднюю полезность, или ожидаемую полезность, структуры потребления ().

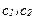По этой причине, мы называем функцию полезности, имеющую конкретную описанную здесь форму функцией ожидаемой полезности или, иногда, функцией полезности фон Нейманна-Моргенштерна. [1]

Говоря, что предпочтения потребителя могут быть представлены с помощью функции ожидаемой полезности, или что предпочтения потребителя обладают свойством ожидаемой полезности, мы подразумеваем, что можно выбрать функцию полезности, имеющую вышеописанную аддитивную форму. Конечно, мы могли бы выбрать и другую форму - любое монотонное преобразование функции ожидаемой полезности есть функция полезности, описывающая те же самые предпочтения. Но аддитивная форма представления предпочтений оказывается особенно удобной. Если предпочтения потребителя описываются функцией 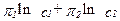, то они также могут быть описаны функцией 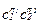. Однако, последняя форма представления предпочтений не обладает свойством ожидаемой полезности, в то время. как предыдущая - обладает.

С другой стороны, функцию ожидаемой полезности можно подвергнуть монотонным преобразованиям различного рода и при этом она по-прежнему будет обладать свойством ожидаемой полезности. Мы говорим, что функция v(u) является положительным линейным преобразованием, если она может быть записана в форме:

v(u)=au+b, где a>0. Положительное линейное преобразование означает просто умножение на положительное число и прибавление константы. Оказывается, если подвергнуть функцию ожидаемой полезности положительному линейному преобразованию, то полученная в результате этого функция не только будет представлять те же самые предпочтения (что очевидно, поскольку линейное преобразование - не что иное, как особый вид монотонного преобразования), но и по-прежнему будет обладать свойством ожидаемой полезности.

Экономисты говорят, что функция ожидаемой полезности "определяется с точностью до монотонного преобразования". Это означает просто, что к ней можно применить линейное преобразование и получить другую функцию ожидаемой полезности. представляющую те же самые предпочтения. Однако, преобразование любого другого рода разрушит свойство ожидаемой полезности.

Дата добавления: 2014-01-06