
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 3. Напряженность и потенциал. Основные теоремы электростатического поля.
|
|
|
|
Так как поле - вид материи, непрерывно распределенный в пространстве, для его характеристики вводят специальные функции координат (функции точки). А так как электростатическое поле является потенциальным (его силы – консервативны), то его можно характеризовать и силовой - напряженностью  , и энергетической - потенциалом j - величинами (полевыми функциями).
, и энергетической - потенциалом j - величинами (полевыми функциями).
Линейная связь сил электростатического взаимодействия с величинами зарядов позволяет ввести силовую характеристику ЭСП - напряженность  - как удельную силу, т. е. силу, действующую со стороны поля на единичный неподвижный положительный заряд в данной точке поля:
- как удельную силу, т. е. силу, действующую со стороны поля на единичный неподвижный положительный заряд в данной точке поля:
 =
= 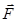 /q Þ единица напряженности [Н/Кл].
/q Þ единица напряженности [Н/Кл].
Т. к. F ~ q, то отношение  /q =
/q =  - не зависит от значения заряда q и характеризует поле само по себе (силу поля) в данной его точке.
- не зависит от значения заряда q и характеризует поле само по себе (силу поля) в данной его точке.
Выражение для напряженности  поля неподвижного точечного заряда q, получим из
поля неподвижного точечного заряда q, получим из
закона Кулона, из силы взаимодействия его с пробным зарядом q¢:
 =
=  /q¢ = [(kqq¢/r2)×
/q¢ = [(kqq¢/r2)×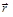 /r]¤q¢ = (kq/r3)×
/r]¤q¢ = (kq/r3)×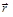 Þ Е = k|q|/r2
Þ Е = k|q|/r2
Важным положением в электростатике является известный еще из механики принцип
суперпозиции (или принцип наложения) сил, выражающий независимость их действия при наличии нескольких сил. B электростатике его обычно называют принципом суперпозиции электростатических полей, и он выражает характеристики результирующего ЭСП при наличии нескольких источников (зарядов). Согласно этому принципу, при наличии нескольких зарядов напряженность 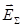 создаваемого ими результирующего ЭСП определяется векторной суммойнапряженностей
создаваемого ими результирующего ЭСП определяется векторной суммойнапряженностей 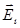 полей, которые бы создавал каждый из этих зарядов в отдельности:
полей, которые бы создавал каждый из этих зарядов в отдельности: 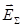 = S
= S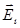 .
.
Чтобы ввести энергетическую характеристику ЭСП – потенциал j, необходимо сначала убедиться в потенциальном характере ЭСП. Для этого нужно показать, что силы ЭСП являются консервативными, то есть их работа по перемещению заряда не зависит от формы траектории. Для простоты составим выражение для работы А12 перемещения пробного заряда q¢ в поле неподвижного точечного заряда q:
А12 =  =
=  =
= 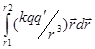 = kqq¢
= kqq¢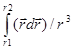 = kqq¢
= kqq¢ = kqq¢(1/r1 - 1/r2) = q¢(j1 - j2).
= kqq¢(1/r1 - 1/r2) = q¢(j1 - j2).
Получили выражение, из которого следует, что работа А12 сил ЭСП точечного заряда q по перемещению пробного заряда q¢ не зависит от формы траектории перемещения, а определяется лишь его начальным и конечным положениями, задаваемых координатами r1 и r2. В качестве энергетической характеристики этого положения (точки поля) и выбирается скалярная величина, называемая потенциалом j. Для точечного заряда j = kq/r.
Полученный результат о потенциальном характере ЭСП неподвижного точечного заряда можно обобщить на ЭСП, создаваемое произвольной системой неподвижных зарядов.
Энергетическая характеристика ЭСП - потенциал j может быть получена из известного в механике выражения, связывающего силу и потенциальную энергию, в соответствии с которым, сила есть антиградиент потенциальной энергии (или проекция силы на некоторое направление равна быстроте убыли потенциальной энергии Wп в данном направлении).
 = - grad Wп Þ
= - grad Wп Þ 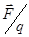 = - grad Wп/q Þ
= - grad Wп/q Þ  = - grad j
= - grad j
где за потенциал j принято отношение потенциальной энергии взаимодействия заряда с полем к величине заряда: j = Wп/q - удельная по заряду потенциальная энергия, то есть потенциальная энергия единичного положительного заряда в данной точке поля, измеряемая в вольтах:о
[Дж/Кл = В]. Или из Fх = - ¶Wп/¶х Þ Ех = - ¶j/¶х [В/м]
Из взаимосвязи силовой и энергетической характеристик ЭСП получает иное выражение и трактовку единица напряженности. Будучи антиградиентом потенциала, выражая своей проекцией быстроту убыли потенциала в соответствующем направлении, напряженность, наряду с исходным выражением  =
=  /q, определяющим ее как удельную силу (в расчете на единицу заряда), измеряется и в В/м. Эта единица показывает, на сколько вольт убывает потенциал на единице длины в соответствующем направлении.
/q, определяющим ее как удельную силу (в расчете на единицу заряда), измеряется и в В/м. Эта единица показывает, на сколько вольт убывает потенциал на единице длины в соответствующем направлении.
Двоякая интерпретация может быть дана и энергетической характеристике ЭCII - потенциалу j. С одной стороны, потенциал j = Wп/q - представляет собой удельную потенциальную энергию ЭСП в данной точке, т. е. потенциальную энергию, которую приобретает в данной точке поля положительный единичный заряд. С другой стороны, поскольку потенциальная энергия (энергия взаимодействия) определяется неоднозначно, с точностью до константы, а ее изменение (убыль) равно работе консервативных сил (какими и являются силы ЭСП), то и потенциал j может быть выражен через работу сил ЭСП по перемещению единичного положительного заряда из данной точки на бесконечность (потенциал точки, достаточно удаленной от источников поля может быть принят равным нулю):
А12 = q(j1 - j2) Þ j1 - j2 = А12/q, или, при j2 ® 0 j1 = А1¥/q.
Из выражения j1 - j2 = А12/q следует, что разность потенциалов двух точек поля есть величина, измеряемая работой сил ЭСП по перемещению положительного единичного заряда из одной точки в другую.
Для однородного ЭСП, напряженность  в котором во всех точках одинакова, взаимосвязь между силовой и энергетической характеристиками упрощается и становится более наглядной:
в котором во всех точках одинакова, взаимосвязь между силовой и энергетической характеристиками упрощается и становится более наглядной:
Ех = - Dj/Dх = (j1 - j2)/(х2 - х1)
Обратный переход от напряженности к разности потенциалов, выражается интегральным соотношением: из dj = - Ехdх Þ
Dj = j2 - j1 =  или j1 - j2 =
или j1 - j2 = 
Для однородного поля: j1 - j2 = Ех(х2 – х1).
Для наглядности ЭСП изображают с помощью силовых линий - касательные, к которым совпадают с направлением вектора  в каждой точке поля, а их густота пропорциональна численному значению напряженности ЭСП в данном месте, и с помощью эквипотенциальных поверхностей, все точки которых имеют одинаковый потенциал. Характерным для ЭСП является перпендикулярность силовых линий эквипотенциальным поверхностям. Это следует из того, что вдоль эквипотенциальной поверхности j = const, то есть dj = 0, а значит проекция Еt вектора
в каждой точке поля, а их густота пропорциональна численному значению напряженности ЭСП в данном месте, и с помощью эквипотенциальных поверхностей, все точки которых имеют одинаковый потенциал. Характерным для ЭСП является перпендикулярность силовых линий эквипотенциальным поверхностям. Это следует из того, что вдоль эквипотенциальной поверхности j = const, то есть dj = 0, а значит проекция Еt вектора  на эквипотенциальную поверхность Еt = - dj/dt = 0. Отсюда вектор
на эквипотенциальную поверхность Еt = - dj/dt = 0. Отсюда вектор  перпендикулярен эквипотенциальной поверхности.
перпендикулярен эквипотенциальной поверхности.
Характерным для ЭСП является также то, что его силовые линии - разомкнуты. Они имеют начало - на положительных зарядах и конец - на отрицательных зарядах или в бесконечности. Замкнутость силовой линии означала бы неравенство нулю работы сил ЭСП по замкнутой траектории, совпадающей с силовой линией, что противоречит его потенциальному характеру.
Силовые линии направлены в сторону убыли потенциала, от большего его значения к меньшему. Формально это следует из взаимосвязи напряженности и потенциала, в соответствии, с которой напряженность есть антиградиент потенциала, а градиент, по определению, есть вектор, направленный в сторону наибыстрейшего возрастания функции (в данном случае – потенциала).
В математическом плане ЭСП, являясь векторным потенциальным полем, полностью
характеризуется двумя теоремами, которые в интегральной форме записываются для циркуляции и потока вектора поля (в данном случае - вектора  ).
).
Циркуляция есть криволинейный интеграл от векторной функции поля по замкнутому контуру. Принимая во внимание смысл вектора  =
=  - сила, действующая на положительный единичный заряд, для циркуляции вектора
- сила, действующая на положительный единичный заряд, для циркуляции вектора  получаем:
получаем:  =
= 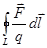 =
=  =
= 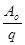 - работа сил ЭСП по перемещению положительного единичного заряда по замкнутой траектории (контуру L). В силу потенциального характера ЭСП работа его сил (являющихся консервативными) по замкнутому контуру нулю. Отсюда следует и теорема о циркуляции вектора
- работа сил ЭСП по перемещению положительного единичного заряда по замкнутой траектории (контуру L). В силу потенциального характера ЭСП работа его сил (являющихся консервативными) по замкнутому контуру нулю. Отсюда следует и теорема о циркуляции вектора  : циркуляция вектора напряженности электростатического поля равна нулю:
: циркуляция вектора напряженности электростатического поля равна нулю:  =
= 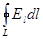 = 0
= 0
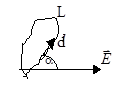 Эта теорема является следствием центрального (радиального) характера сил ЭСП (
Эта теорема является следствием центрального (радиального) характера сил ЭСП (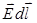 = E×d l ×cos a = E l d l, где Е l = Еcos a - проекция вектора
= E×d l ×cos a = E l d l, где Е l = Еcos a - проекция вектора
на направление d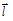 ). Из нее следует разомкнутый характер силовых линий ЭСП; в противном случае, перемещая заряд вдоль замкнутой силовой
). Из нее следует разомкнутый характер силовых линий ЭСП; в противном случае, перемещая заряд вдоль замкнутой силовой
линии, совершали бы ненулевую работу, что противоречит условию потенциальности ЭСП.
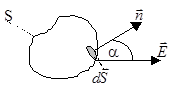 Второй важнейшей теоремой ЭСП является теорема о потоке вектора
Второй важнейшей теоремой ЭСП является теорема о потоке вектора  называемая теоремой Остроградского-Гаусса, иногда - просто теоремой Гаусса. Под потоком Ф вектора через некоторую поверхность понимают поверхностный интеграл от вектора через соответствующую поверхность. Наглядно поток вектора через какую-либо поверхность представляет собой скалярную характеристику векторного поля, которая пропорциональна числу силовых линий, пронизывающих соответствующую поверхность. Через элементарно малую поверхность dS, которой можно придать смысл вектор-площадки[1] d
называемая теоремой Остроградского-Гаусса, иногда - просто теоремой Гаусса. Под потоком Ф вектора через некоторую поверхность понимают поверхностный интеграл от вектора через соответствующую поверхность. Наглядно поток вектора через какую-либо поверхность представляет собой скалярную характеристику векторного поля, которая пропорциональна числу силовых линий, пронизывающих соответствующую поверхность. Через элементарно малую поверхность dS, которой можно придать смысл вектор-площадки[1] d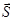 , поток dФЕ вектора
, поток dФЕ вектора  будет равен произведению: dФЕ =
будет равен произведению: dФЕ = 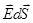 = Е×dS×cos a = ЕndS, где a - угол между вектором
= Е×dS×cos a = ЕndS, где a - угол между вектором  и внешней единичной нормалью
и внешней единичной нормалью  к площадке
к площадке 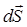 , а Еn = Еcos a - проекция вектора
, а Еn = Еcos a - проекция вектора  на направление нормали
на направление нормали  . Полный же поток ФЕ вектора
. Полный же поток ФЕ вектора  сквозь поверхность S определится поверхностным интегралом: ФЕ =
сквозь поверхность S определится поверхностным интегралом: ФЕ = =
=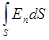
В соответствии с этим соотношением напряженности  можно придать смысл поверхностной плотности потока вектора
можно придать смысл поверхностной плотности потока вектора  (потока силовых линий), то есть величины, пропорциональной густоте силовых линий, то есть их числу, пронизывающих единичную площадку. Теорема о потоке вектора напряженности ЭСП - теорема Остроградского - Гаусса утверждает, что поток ФЕ вектора
(потока силовых линий), то есть величины, пропорциональной густоте силовых линий, то есть их числу, пронизывающих единичную площадку. Теорема о потоке вектора напряженности ЭСП - теорема Остроградского - Гаусса утверждает, что поток ФЕ вектора  через любую замкнутую поверхность S не зависит от размера и формы поверхности, а определяется лишь полным электрическимзарядом qå, находящимся внутри замкнутой поверхности, будучи численно равным этому заряду, деленному на электрическую постоянную eо:
через любую замкнутую поверхность S не зависит от размера и формы поверхности, а определяется лишь полным электрическимзарядом qå, находящимся внутри замкнутой поверхности, будучи численно равным этому заряду, деленному на электрическую постоянную eо:
ФЕ =  = qS/eо.
= qS/eо.
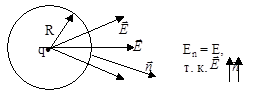 Покажем на примере точечного заряда q справедливость теоремы Остроградского - Гаусса.
Покажем на примере точечного заряда q справедливость теоремы Остроградского - Гаусса.
Окружим точечный заряд замкнутой поверхностью, для простоты в виде сферы радиуса R и вычислим поток вектора  от точечного заряда через эту сферическую поверхность. Выражение для напряженности Е поля точечного заряда q получим из закона Кулона, из силы взаимодействия его с пробным зарядом q¢:
от точечного заряда через эту сферическую поверхность. Выражение для напряженности Е поля точечного заряда q получим из закона Кулона, из силы взаимодействия его с пробным зарядом q¢:
 =
=  /q¢ = (kqq¢/r2)q¢ Þ Е = kq/r2 (k = 1/4peо)
/q¢ = (kqq¢/r2)q¢ Þ Е = kq/r2 (k = 1/4peо)
Подставляя это выражение в формулу для потока вектора  , получим:
, получим:
ФЕ =  =
=  = Е
= Е = ЕS = (kq/R2)4pR2 = q/eо.
= ЕS = (kq/R2)4pR2 = q/eо.
Действительно, поток ФЕ вектора  сквозь сферическую поверхность S равен заряду, находящемуся внутри поверхности, деленному на eо. Такая связь характеристики ЭСП (потока вектора
сквозь сферическую поверхность S равен заряду, находящемуся внутри поверхности, деленному на eо. Такая связь характеристики ЭСП (потока вектора  ) с источниками его порождающими (с зарядами), с одной стороны, является важным законом природы (следствием закона «обратных квадратов» в зависимости сил электрического взаимодействия точечных зарядов), а с другой – выступает методом для решения основной задачи электростатики - расчета характеристик поля по известному распределению его источников - электрических зарядов. Это наглядно видно на примере точечного заряда и случая сферической поверхности, поток вектора
) с источниками его порождающими (с зарядами), с одной стороны, является важным законом природы (следствием закона «обратных квадратов» в зависимости сил электрического взаимодействия точечных зарядов), а с другой – выступает методом для решения основной задачи электростатики - расчета характеристик поля по известному распределению его источников - электрических зарядов. Это наглядно видно на примере точечного заряда и случая сферической поверхности, поток вектора  через которую, пропорционален ее площади и, соответственно, квадрату ее радиуса.
через которую, пропорционален ее площади и, соответственно, квадрату ее радиуса.
Обобщая теорему о потоке вектора  ЭСП на произвольную систему зарядов, получим:
ЭСП на произвольную систему зарядов, получим:
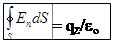
где qå = åq i - для дискретного распределения зарядов, создающих ЭСП (и поток ФЕ).

 t d l - для линейного,
t d l - для линейного,
и qå = 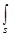 sdS - поверхностного, - непрерывных распределений заряда по телу.
sdS - поверхностного, - непрерывных распределений заряда по телу.
 rdv - объемного
rdv - объемного
и где t = dq/d l - линейная, s = dq/dS - поверхностная и r = dq/dv - объемная плотности заряда, измеряемые в Кл/м, Кл/м2 и Кл/м3, соответственно. В случае равномерного распределения заряда производные заменяются отношениями: t = q/ l, s = q/S и r = q/V и представляют собой соответственно заряд единицы длины, единицы площади и единицы объема заряженного тела.
Учитывая, что в диэлектрической среде электрическое поле ослабляется в e раз, вводят вспомогательную силовую характеристику  , называемую электрическим смещением или вектором индукции электрического поля, связанную с основной силовой характеристикой ЭСП - вектором напряженности
, называемую электрическим смещением или вектором индукции электрического поля, связанную с основной силовой характеристикой ЭСП - вектором напряженности  , следующим соотношением:
, следующим соотношением:  = eоe
= eоe
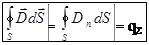 Эта величина характеризует силу ЭСП в вакууме, т. е. ЭСП самого по себе, без учета среды. Она облегчает расчет характеристик ЭСП в неоднородных диэлектрических средах.
Эта величина характеризует силу ЭСП в вакууме, т. е. ЭСП самого по себе, без учета среды. Она облегчает расчет характеристик ЭСП в неоднородных диэлектрических средах.
Использование вектора  позволяет придать более простой вид теореме Остроградского - Гаусса:
позволяет придать более простой вид теореме Остроградского - Гаусса:
- поток вектора электрического смещения через любую замкнутую поверхность не зависит от размеров и формы этой поверхности, а определяется алгебраической суммой qå свободных зарядов, находящихся внутри этой поверхности, и равен значению этого заряда.
ЭСП полностью характеризуется двумя теоремами: теоремой о циркуляции и теоремой о потоке вектора  . Эти теоремы образуют полную систему уравнений ЭСП в интегральной форме.
. Эти теоремы образуют полную систему уравнений ЭСП в интегральной форме.
В решении конкретных задач электростатики часто удобным оказывается использование энергетической характеристики - потенциала j и вспомогательной силовой характеристики - вектора индукции ЭСП -  . При этом необходимыми оказываются уравнения связи силовой и энергетической характеристик ЭСП
. При этом необходимыми оказываются уравнения связи силовой и энергетической характеристик ЭСП  = - grad j и основной и вспомогательной силовых характеристик ЭСП
= - grad j и основной и вспомогательной силовых характеристик ЭСП  = eоe
= eоe
Фактически обе теоремы ЭСП эквивалентны одному закону Кулона и, по сути, являются его следствиями, - следствиями устанавливаемых этим законом основных свойств ЭСП - его потенциальности (консервативности сил ЭСП) и закона "обратных квадратов" в зависимости сил от расстояния.
Для перехода к дифференциальной форме записи теоремы о циркуляции воспользуемся
известной из векторного анализа теоремой Стокса, связывающей циркуляцию вектора с поверхностным интегралом от ротора этого вектора:
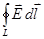 =
=  ,
,
гдеS – поверхность, ограниченная контуром L. Под ротором вектора понимают векторный дифференциальный оператор, задаваемый следующим образом:
rot  =
= 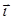 (¶Еу/¶z - ¶Еz/¶у) +
(¶Еу/¶z - ¶Еz/¶у) + 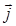 ( ¶Еz/¶х - ¶Ех/¶z) +
( ¶Еz/¶х - ¶Ех/¶z) + 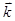 (¶Еx/¶y - ¶Еy/¶x)
(¶Еx/¶y - ¶Еy/¶x)
Физический смысл ротора вскрывают, устремляя поверхность S к нулю. В пределах достаточно малой поверхности ротор вектора можно считать постоянным и вынести за знак интеграла:
 = rot
= rot ×
× 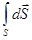 = rot
= rot ×S.
×S.
Тогда, согласно теореме Стокса:rot  = (1/S)
= (1/S)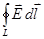 при S ® 0.
при S ® 0.
Отсюда ротор вектора можно определить как поверхностную плотность циркуляции этого вектора.
Так как в ЭСП циркуляция вектора  равна нулю, то равен нулю и ротор вектора
равна нулю, то равен нулю и ротор вектора  :
:
rot  = 0.
= 0.
Это уравнение и есть дифференциальная форма теоремы о циркуляции вектора  в ЭСП.
в ЭСП.
Для перехода к дифференциальной форме записи теоремы Остроградского – Гаусса воспользуемся известной из векторного анализа теоремой Гаусса, связывающей поток вектора по замкнутой поверхности с интегралом от дивергенции этого вектора по объему, заключенному в этой поверхности:
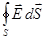 =
= 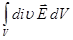 .
.
Под дивергенцией вектора понимают скалярный дифференциальный оператор (совокупность производных), задаваемый следующим образом:
div  = ¶Ех/¶х + ¶Еу/¶у + ¶Еz/¶z.
= ¶Ех/¶х + ¶Еу/¶у + ¶Еz/¶z.
Физический смысл дивергенции вскрывают, устремляя объем V к нулю. В пределах достаточно малого объема дивергенцию вектора можно считать постоянной и вынести за знак интеграла:
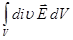 = div
= div ×
×  = (1/V) div
= (1/V) div  . Тогда, согласно теореме Гаусса,
. Тогда, согласно теореме Гаусса,
div  = (1/V)
= (1/V) 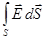 при V ® 0.
при V ® 0.
Отсюда дивергенцию вектора можно определить как объемную плотность потока этого вектора.
Соотнося теорему Остроградского – Гаусса 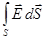 = qå/eо = (1/eо)
= qå/eо = (1/eо) и теорему Гаусса
и теорему Гаусса 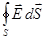 =
= 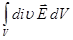 , видим, что левые их части равны друг другу. Приравнивая их правые части, получаем: div
, видим, что левые их части равны друг другу. Приравнивая их правые части, получаем: div  = r/eо.
= r/eо.
Это уравнение и представляет собой дифференциальную форму теоремы Остроградского – Гаусса.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 935; Нарушение авторских прав?; Мы поможем в написании вашей работы!