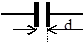Электроемкость проводника. Конденсаторы

Лекция 4. Конденсаторы. Электроемкость. Энергия и объемная плотность энергии электрического поля.

Потенциал j, приобретаемый уединенным проводником при сообщении ему заряда q, прямо пропорционален заряду q и зависит от размеров и формы проводника, а также от окружающих его тел и полей (электрических). Отношение же С = q/j, не зависит ни от заряда q, ни от потенциала j и характеризует способность проводника (назы­ваемую электроемкостью, или просто емкостью) поддерживать постоянным определенное отно­шение заряда на проводнике к его потенциалу или, иначе - удерживать (накапливать) определенный заряд при заданном потенциале. Численно емкость проводника равна заряду, при котором проводник приобретает единичный потенциал (или, изменяет его на единицу).

Единицей электроемкости является фарад: 1 Ф = 1 Кл/1 В.

Для сферического проводника радиусом R и зарядом q потенциал j равен: j = kq/R и емкость С_сф = q/j = q/(kq/R) = R/k = 4pe_оR.

Для устранения зависимости электроемкости от окружающих тел и электрических полей и накопления значительных зарядов применяют устройства в виде системы проводников, называе­мые конденсаторами. Простейший тип конденсатора состоит из двух проводников (называемых электродами или обкладками), разделенных диэлектриком. В зависимости от конфигурации элек­тродов различают плоские, сферические, цилиндрические конденсаторы. Они концентрируют все свое ЭСП в пространстве между обкладками, куда не проникает внешнее ЭСП, которое, поэтому и не оказывает на него никакого влияния.

Заряжение обкладок конденсатора зарядом ± q сопровождается появлением между ними разности потенциалов Dj, прямо поропорциональной сообщенному заряду q. Емкость конденсатора определяется как отношение заряда q одной из его разноименно заря­женных обкладок, к разности потенциалов между ними:

С = q/(j₂ - j₁) = q/Dj или С = q/U

Она характеризует способность конденсатора поддерживать постоянным определенное отношение заряда на обкладках к разности потенциалов между ними или, иначе -удерживать (накапливать) определенный заряд на обкладках при заданной (например, единичной) разности потенциалов между ними. Численно емкость конденсатора равна заряду, сообщение которого обкладкам вызывает единичную разность потенциалов между ними (или ее единичное изменение).

Отсутствие влияния внешних тел и электрических полей на емкость конденсатора, т. е. на отношение q/Dj объясняется тем, что все ЭСП конденсатора (его разноименно заряженных пластин) сосредоточено внутри него, между его обкладками и заэкранировано ими. Сна­ружи поля конденса­тора нет и поэтому он "безразличен" к наличию или отсутствию внешних тел или полей.

Ранее, при применении теоремы Остроградского-Гаусса для вычисления напряженности ЭСП двух разноименно заряженных пла­стин, уже было получено выражение дляэлектроемкости плос­кого конденсатора: С = e_оeS/d

где S - площадь одной обкладки (пластины) конденсатора;

d - расстояние между обкладками конденсатора;

e - диэлектрическая проницаемость среды между обкладками.

У конденсатора с большей диэлектрической проницаемостью e диэлектрика между обклад­ками емкость С больше потому, что при неизменном заряде q на обкладках диэлектрик уменьшает в e раз напряженность ЭСП, а соответст­венно и разность потенциалов Dj = Еd между обкладками, так что отношение q/Dj = С – возрастает в e раз.

У конденсатора с большей площадью S обкладок емкость С больше потому, что при одинаковом их заряде q поверхностная плотность s = q/S, а, соответственно и напряженность Е = s/e_оe и разность потенциалов Dj = Еd между обкладками меньше, то есть отношение q/Dj = С - больше.

С увеличением расстояния d между обкладками емкость С конденсатора уменьшается (при прочих одинаковых параметрах) потому, что при одинаковом заряде q на обкладках и, соответственно, при одинаковой плотности заряда s = q/S и напряженности Е = s/e_оe, разность потен­циалов между обкладками Dj = Еd возрастает, а отношение С = q/Dj убывает обратно пропорцио­нально расстоянию d.

На практике в целях получения необходимой электроемкости (и рабочего напряжения) кон­денсаторы часто соединяют в батареи с последовательным и/или параллельным соединением.

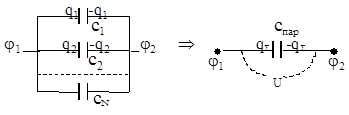При параллельном соединении все конденсаторы имеют единое общее начало и общий еди­ный конец. При этом на каж­дом из конденсаторов одинакова разность потенциалов Dj_i = Dj = const, а полный заряд q_S батареи равен сумме Sq_i зарядов на каждом из конденсато­ров. Ре­зульти­рующая емкость параллельного соеди­нения N конденсаторов равна:

С = q_S/Dj_S = Sq_i/Dj_i = q₁/Dj + q₂/Dj + … + q_N/Dj = С₁ + С₂ +... + С_N = SС_i

- результирующая емкость равна сумме емко­стей, составляющих батарею кон­денсаторов.

При последовательном соединении конденсаторов (в цепочку, один за другим) одинаковым является заряд q_i = q = q_S на каждом из конденсаторов, а результирующая разность потенциалов Dj_S равна сумме SDj_i разностей потенциалов на каждом из конденсаторов[2]. И результирующая емкость батареи из N последователь­ного соединенных конденсаторов будет равна:

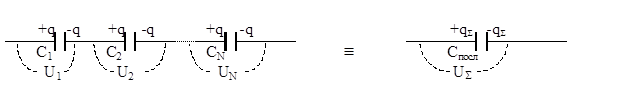С_посл = q_S/Dj_S = q/Dj_S; 1/С_посл = Dj_S/q = SDj_i/q = Dj₁/q + Dj₂/q +... + Dj_N/q = 1/C₁ + 1/C₂ +... + 1/C_N = S1/C_i Þ 1/C_посл = S(1/С_i) -

- результирующая обратная емкость 1/C_посл последовательного соединения конденсаторов равна сумме S(1/С_i) обратных емкостей, составляющих батарею конденсаторов (и оказывается меньше наименьшей из складываемых емкостей).

Для простейшей батареи из двух (N = 2) конденсаторов С_посл = С₁×С₂/(C₁ + C₂).

Энергия заряженного конденсатора и проводника. Объемная плотность энергии ЭСП.

Электрическое поле, являясь видом материи, обладает энергией - универсальной мерой дви­жения и взаимодействия. Заряжение (электризация) проводника всегда связано с совершением работы по преодолению кулоновских сил отталкивания между одноименными зарядами, которая идет на увеличение его электрической энергии. Для переноса элементарно малого заряда dq из бесконеч­ности на проводник требуется совершить элементарную работу

dА¢ = dq×j = q×dq/С Þ А^¢ = q²/2С = Сj²/2 = qj/2.

Аналогично, для конденсатора работа по переносу заряда dq с одной обкладки на другую:

dА¢ = dq(j₁ – j₂) = q×dq/С Þ W_с = q²/2С = С×Dj²/2 = q×Dj/2.

Учитывая, что конденсатор - это система из двух заряженных проводников с зарядами
q₁ = - q₂ = q, перепишем формулу для энергии электрического поля конденсатора:

W_с = q(j₁ – j₂) = (q₁×j₁ + q₂×j₂)/2.
И можно показать, что для системы из N неподвижных проводников их полная энергия

W_S =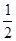

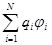
Энер­гия конденсатора сосредоточена в пространстве между пластинами конденсатора, т. е. в объеме V = S×d.

Объемная плотность энергии ЭСП, т. е. энергия, приходящаяся на единицу объема, равна:

w_э = W_э/V = q²/2CV = s²S²d/(2e_оeSV) = s²S²d/(2e_оeSSd) = s²/2e_оe = e_оeЕ²/2

Материальным носителем энергии заряженного конденсатора является не конденсатор
непо­средственно и не заряды на нем, а его электрическое поле, заполняющее пространство объемом V = S×d внутри конденсатора и распределенное в нем с объемной плотностью:

w_э = e_оeЕ²/2 [Дж/м³]

Энергия ЭСП заряженных проводников, выражаемая формулой W_э = С×j²/2, также распределена в пространстве с объемной плотностью

w_э = e_оeЕ²/2

Лекция 5. Электрический ток. Сила тока и плотность тока. Законы Ома.

Электрический ток является одним из наиболее распространенных источников магнитного поля, поэтому, прежде чем переходить к изучению магнитного поля, целесообразно изучить основ­ные характеристики и законы электрического тока. Кроме того, эффекты, связанные с электриче­ским током, чрезвычайно широко используются в современной биологии.

Дата добавления: 2014-01-06