Особенности напряженно-деформированного состояния тонкостенных конструкций покрытий.

Классическая теория расчета оболочек основана на двух гипотезах: линей­ный элемент, нормальный к срединной поверхности оболочки, остается прямым и нормальным к данной поверх­ности после деформации конструкции; напряжения на площадках, параллельных срединной поверхности, не учитываются. Применение этих гипотез приводит к рас­четным дифференциальным уравнениям высокого порядка относительно неизвестных функций. Уравнения получают в частных производных по двум переменным координатам точек срединной поверхности. Поскольку расчет сложный, принимают дополнительные допущения. Например, оболочки положительной гауссовой кривизны рассчитывают по безмоментной теории, при расчете по­логих оболочек криволинейные координаты точек срединной поверхности заменяют прямолинейными координатами проекций этих точек на плоскость основания и т.д.

Теоретические и экспериментальные исследования свидетельствуют, что железобетонные пространственные конструкции могут работать под нагрузкой в упругом и упругопластическом состояниях. В общем случае в нормальных сечениях оболочек возникают нормальные силы N_x и N_y, сдвигающие силы Q_xy и Q_yх, изгибающие моменты М _х и М_у, поперечные силы Q_x и Q_y, а также крутящие моменты Т_х и Т_у. Все эти усилия относятся к единице длины сечения (рис. 2). Расчет оболочек начинают с состояния статических уравнений, т. е. урав­нений равновесия. К ним добавляют геометрические уравнения, связывающие линейные и угловые деформации, а также кривизны срединной поверхности оболочек с их перемещениями. Связь между статическими и гео­метрическими уравнениями выражают физическими уравнениями, которые представляют собой обобщенный закон Гука для объемного напряженного состояния ма­териалов. Наличие трещин в бетоне оценивают системой физических уравнений, основанных на теории Н. И. Карпенко. Статический расчет тонкостенных пространствен­ных конструкций с учетом физической и геометрической нелинейности оболочки сложен, поэтому такой расчет оболочек производят с использованием численного мо­делирования на ЭВМ путем реализации метода конеч­ных элементов и других численных методов.

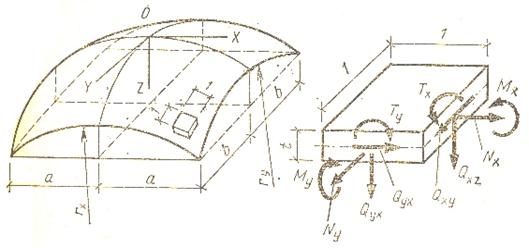
Усилия, действующие в тонкой оболочке

Дата добавления: 2014-01-06