Основные характеристики и законы постоянного тока

При приложении к проводнику постоянной разности потенциалов в нем возникает под дейст­вием сил ЭСП уравновешивающий поток заряженных микрочастиц, который и называется электри­ческим током. Количественными характеристиками, мерами этого потока являются:

1) скалярная и интегральная по площади поперечного сечения мера быстроты переноса заряда, называе­мая силой тока: I = dq/dt или, для постоянного тока, I = q/t [1 Кл/с = 1 А]. Сила тока представляет собой поток заряда в проводнике, т. е. численно равна заряду, пере­носимому через поперечное сече­ние проводника за еди­ницу времени.

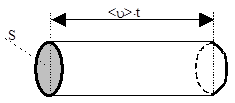2) векторная и локальная (дифференциальная) по площади поперечного сечения проводника мера быст­роты переноса заряда, называемая плотностью тока: j = I/S_^ [1 А/1 м²] - поверхностная плотность потока заряда.

За время t через поперечное сечение проводника пройдут все носители заряда, содержащиеся в объеме цилиндра высотой <u>t. Их число N = nV = nS<u>t, где n – концентрация свободных носителей заряда в проводнике и <u> - средняя скорость их направленного движения.Они перенесут заряд q_S = qN = qnS<u>t и создадут ток силой I = q_S/t = qnS<u> и плотность тока j = I/S = qn<u>, где q – заряд одной свободной частицы.

Опытным путем были установлены два основных закона постоянного тока для однородного (не содержащего источников тока) участка цепи

1) Закон Ома. При приложении к однородному[3] участку цепи разности потенциалов Dj в нем воз­никает электрический ток, сила I которого прямо пропорциональна Dj и обратно пропорциональна сопротивлению участка цепи: I = Dj/R

Из этого закона выражается и получает интерпретацию одно из важнейших понятий учения об электрическом токе - понятие э лектросопротивления:

R = Dj/I [1В/1А = 1 Ом].

Электросопротивление однородного участка цепи, вследствие прямо пропорциональной зависимости между силой тока I и разностью потенциалов Dj, не зависит ни от I, ни от Dj, а опреде­ляется лишь их отношением. С ростом разности потенциалов Dj на концах проводника прямо пропорционально возрастает сила тока I, протекающего через него, а отношение разности потенциалов к силе тока Dj/I, которое и есть сопротивление проводника, остается неизменным. Сопротивление участка цепи (резистора) и есть способность его поддерживать постоянным определенное отношение между разностью потенциалов на его концах и силой тока, протекающего через него. Численно электросопротивление резистора равно разности потенциалов на нем, обусловливающей ток единичной силы в нем. Сопротивлением эта величина названа потому, что без противодействия направленному потоку заряженных частиц постоянная разность потенциалов, а, соответственно и постоянная напряженность, т. е. сила, действующая на заряженные частицы, приводили бы к непре­рывному возрастанию их скорости и, соответственно - силы тока, чего не имеет места на практике. В основе физического механизма ограничения скорости носителей заряда в металличе­ском провод­нике лежит, как показано будет ниже в классической теории электропроводности метал­лов, рассея­ние ускоряемых электрическим полем носителей заряда - электронов на разного рода несовершен­ствах состава и структуры материала (тепловых колебаниях узлов кристаллической решетки, примесях, вакансиях и т. п.).

Наряду с приведенной выше так называемой интегральной формой закона Ома, существует еще и дифференциальная (лучше сказать - локальная) форма закона Ома. Для ее получения подставим в выражение для сопро­тивления вместо интегральных характеристик - разности потенциалов и силы тока, дифференциаль­ные - напряженность и плотность тока:

R = Dj/I = Е l /jS = r l /S, где r = Е/j или j = Е/r

Отношение напряженности Е в проводнике к плотности тока j в нем есть величина постоянная, зависящая лишь от свойств проводника и называемая его удельным электросопротивлением r. Удель­ным сопротивлением называют сопротивление проводника единичных размеров (единичной длины и площади поперечного сечения). Это следует из выражения для электросопротивления однородного проводника:

R = r l /S Þ r = RS/ l [Ом×м/² = Ом×м] Þ r = R при l = 1 м и S = 1м².

Сопротивление однородного проводника R = r l /S прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от рода материала, соответствующей характеристикой которого является его удельное электросопротивление r.

У более длинного про­водника при одинаковой разности потенциалов на концах меньше напряженность ЭСП Е = Dj/ l, а значит и сила F = qЕ, действующая на носители тока в проводнике. Меньшая сила сооб­щает им меньшее ускорение и, соответственно, меньшую среднюю скорость, а, значит, за единицу времени в длинном проводнике пройдет меньший заряд, т. е. ток I меньшей силы. Итак, в длинном проводнике, при той же разности потенциалов на концах, отношение R = Dj/I, которое и выражает собой электросопротивление проводника (участка цепи), больше чем в коротком.

У более толстого проводника (проводника с большей площадью поперечного сечения) при одинаковой с тонким проводником разности потенциалов одинаковой будет напряженность ЭСП внутри проводника и сила, действующая на носители тока. Последние, будут двигаться с одина­ковым ускорением и одинаковой средней скоростью в обоих проводниках, т. е. обеспечат одина­ковую плотность тока - заряд, переносимый за единицу времени через единицу площади попе­речного сечения. Сила же тока I = j×S в толстом проводнике больше чем в тонком и, значит отношение R = Dj/I, т. е. сопротивление, у толстого проводника меньше, чем у тонкого проводника.

Физический механизм влияния r на сопротивление проводника заключается в рассеянии носителей тока на разного рода несовершенствах состава и структуры материала, которое ограничи­вает возрастание скорости носителей тока и определяет тем самым среднюю их скорость, а вместе с ней и силу тока (при фиксированной разности потенциалов).

В электро- и радиотехнике часто приходится иметь дело с последовательным, или парал­лельным соединением участков цепи, обладающих сопротивлением; их часто называют резисто­рами. Получим формулы для расчета результирующего электросопротивления соединения N резисторов:

а) при последовательном соединении

(в цепочку, один за другим) через все

резисторы протекает один и тот же ток I, а результирующая разность потенциалов Dj_S равна сумме SDj_i на каждом из них:

R_посл = Dj_S/I = (Dj₁ + Dj₂ +...+ Dj_N)/I = Dj₁/I + Dj₂/I +...+ Dj_N/I = R₁ + R₂ + R_N = SR_i

- результи­рующее сопротивление равно сумме сопротивлений последовательно соединенных резисторов.

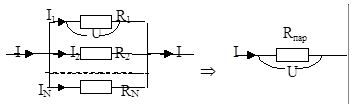б) при параллельном соединении N резисторов одинаковой является разность потенциалов
(j₁ - j₂) на каждом из них, а результирующий ток I_S равен сумме SI_i токов, протекающих через каждый из резисторов.

R_пар = (j₁ - j₂)/I_S = (j₁ - j₂)/(I₁ + I₂ + … + I_N) = 1/(1/R₁ + 1/R₂ + 1/R_N) Þ 1/R_пар = S1/R_i - при параллельном соединении резисто­ров суммируются их обратные сопротивления (у конденсаторов было наоборот).

Для R₁ = R₂ = … = R_N, R_пар = R₁/N. Для N = 2, R_пар = R₁R₂/(R₁ + R₂).

Дата добавления: 2014-01-06