Лекция 6. Электронная теория электропроводности. Закон Ома и Джоуля-Ленца в дифференциальной форме

Закон Джоуля – Ленца. При приложении к однородному участку цепи с сопротивлением R разности потенциалов Dj, в нем протекает элек­трический ток силой I, и за время t на участке цепи выделяется теплота Q, пропорциональная силе тока, разности потенциалов и времени прохождения тока: Q = Dj×I×t.

Тепловая мощность электрического тока, выделяющаяся на участке цепи (на его сопротивлении):

Р = Q/t = IDj = I²R = (Dj)²/R [Дж/с = Вт]

Формально закон Джоуля - Ленца может быть получен как следствие закона Ома:

при пере­носе заряда q за время t по участку цепи с разностью потенциалов Dj = IR совершается работа рав­ная: А = q×Dj = I²Rt, которая и идет на нагрев участка цепи, т. е. выделяется в виде тепла (если уча­сток цепи неподвижен, и в нем отсутствуют химические превращения).

Наряду о приведенной выше интегральной формой закон Джоуля - Ленца имеет, как и закон Ома и дифференциальную форму, справедливую локально, т. е. в точке (в физически бесконечно малом объеме): ее можно получить из интегральной формы, заменяя в ней интегральные харак­теристики - Dj, I, и R на соответствующие дифференциальные – Е, j, и r:

Р = DjI = Е l (j S) = jЕS l = jЕV Þ Р_уд = Р/V = jЕ = Е²/r

Общность законов Ома и Джоуля - Ленца имеет не только формальные, но и глубокие содер­жательные, сущностные основания. Если закон Ома отражает особенности взаимодействия потока заряженных частиц с материалом проводника со стороны ограничения скорости потока заряженных и ускоряемых электрическим полем частиц, то закон Джоуля - Ленца отражает это взаимодействие со стороны передачи энергии ускоренных электрическим полем заряженных частиц, материалу про­водника. Более наглядно эти моменты вскрываются в классической электронной теории элек­тро­проводности металлов (КЭТЭМ). Рассмотрим физику процессов, обусловливающих электросопротивление и джоулев нагрев в металлах, и выведем полученные опытным путем законы Ома и Джоуля - Ленца.Носителями тока в металлах являются коллективизированные (обобществленные) валентные электроны атомов. В узлах их кристаллической решетки металлов находятся положительно заряженные ионы, совершающие хаотические тепловые колеба­ния вокруг положений равновесия. В пространстве между ионами сравнительно свободно переме­щаются отрицательно заряженные электроны, образующие своего рода электронный газ, подчи­няю­щийся, согласно КЭТЭМ, статистике Максвелла - Больцмана.

При наложении внешнего электрического поля с напряженностью на электрон действует сила = q, сообщающая ему ускорение а = /m = q/m. Фактором, ограничивающим рост скорости электронов и ответственным как за электросопротивление (электрическое трение, тормо­жение), так и за джоулев нагрев проводника электрическим полем, является рассеяние электронов (являющихся носителями тока в металлах) на разного рода дефектах, несовершенствах материала (хаотических колеблющихся ионах, примесях, вакансиях и т. п.). В результате такого рассеяния и осуществляется "сброс" скорости и кинетической энергии с ускоренных электрическим полем электронов. Электроны при этом тормозятся, материал же, оказывая сопротивление их потоку, и, принимая на себя энергию движения электронов, повышает свою внутреннюю энергию, нагрева­ется.

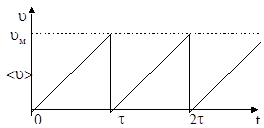
Усредненный характер зависимости скорости электронов от времени можно изобразить в виде пилообразного графика. Скорость электрона ускоренного приложен­ным к проводнику электрическим полем линейно возрастает до тех пор, пока электрон не "столкнется" с какого-либо рода неоднородностью кристалла, не рассеется на ней и не потеряет своей скорости и кинетической энергии. Статистиче­ски усредненное время свободного пробега (от соударения до следующего соударения) обозначено за t.

В среднем можно считать, что электрон движется со скоростью <u> = u_макс/2.

Так как u_макс = аt = qЕt/m, то <u> = qЕt/2m.

При перемещении с такой средней скоростью, через поперечное сечение S проводника за время t пройдет число N носителей, содержащееся в объеме проводника V = S<u> t.

N = nV, где n - концентрация носителей (число их в единице объема). Они перенесут заряд

q_å = q×N = qnV = qn <u> St.

Заряд же переносимый через единицу площади поперечного сечения за единицу времени, т. е. плот­ность тока, равна:

j = q_å/St = qn <u> = qnqЕt/2m = (nq²t/2m)Е = gЕ = Е/r,

где коэффициент пропорциональности между плотностью тока и напряженностью Е есть удельная электропроводность g или обратное ей удельное электросопротивление 1/r:

g = 1/r = nq²t/2m.

Полученная связь между плотностью тока и напряженностью электрического поля и пред­ставляет закон Ома в дифференциальной форме: j = gЕ = Е/r.

Для получения закона Джоуля - Ленца в дифференциальной форме, рассмотрим механизм нагрева проводника электрическим током. Такой нагрев, как правило, осуществляется в результате столкновений (рассеяния) электронов с хаотически колеблющимися ионами в узлах кристалличе­ской решетки, которым электроны и передают накопленную в ускоряющем их электрическом поле кинетическую энергию mu²_макс/2. Электроны здесь играют роль своеобраз­ного трансформатора; воспринимая энергию электрического поля в виде своей кинетической энер­гии, они затем передают ее при соударениях на увеличение амплитуды и соответственно энергии тепло­вых хаотических колебаний ионов в узлах решетки.

3а единицу времени один электрон столкнется 1/t раз и передаст решетке энергию (mu²_макс/2)(1/t). Единице же объема будет передана (выделена) энергия: Р_уд = nmu²_макс/2t.

Подставляя в это выражение u_макс = аt = qЕt/m, получаем:

Р_уд = nmu²_макс/2t = nm(qЕt)²/2tm² = (nq²t/2m)Е² = gЕ² = Е²/r,

т. е. закон Джоуля - Ленца Р_уд = gЕ² = Е²/r - в дифференциальной форме, где r = 2m/nq²t.

Дата добавления: 2014-01-06