Лекция 11. Вынужденные колебания заряда и тока в контуре. Физическая сущность явления резонанса

Для получения незатухающих электромагнитных колебаний в контуре к нему необходимо извне подводить энергию, компенсирующую потери на джоулево тепло в электросопротивлении. Для этого к контуру подключают внешний источник переменного тока, который создает в 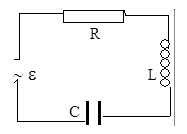нем вынужденные колебания заряда и тока. Рассмотрим особенности вынужденных колебаний в R-L-C контуре при подключении к нему внешнего источника с гармонически изменяющейся ЭДС e = e_мcos wt.

Дифференциальное уравнение колебаний заряда в R-L-C контуре можно получить на основе как энергетического, так и «силового» подходов. С энергетических позиций мощность источника тока Р_и = eI расходуется на изменение электрической и магнитной W_м энергий конденсатора и катушки и на восполнение джоулевых потерь Р_R в электросопротивлении:

Р_и = d/dt(W_э + W_м) + Р_R Þ Р_и = d/dt (q²/2C + LI²/2) + I²R

Произведя преобразования, аналогичные проведенным ранее при анализе свободных и зату­хающих колебаний, получим в итоге каноническую форму дифференциального уравнения вынуж­денных колебаний заряда:

d²q/dt² + 2d×dq/dt + w_о²×q = (e_м/L)cos wt

Полученное уравнение является неоднородным, и его решение состоит из общего решения соответствующего однородного уравнения (с полагаемой нулю правой частью) и частного решения неоднородного уравнения.

Общее решение однородного уравнения было уже рассмотрено и проанализировано ранее при анализе затухающих колебаний. Оно имеет место на этапах установления стационарного режима вынужденных колебаний. В установившемся же режиме характер колебаний заряда будет определяться (навязываться) правой частью неоднородного уравнения, то есть внешней ЭДС, играющей роль вынуждающей силы. Эти вынужденные колебания заряда будут происходить по закону внешней ЭДС (гармоническому), то есть с ее частотой w и с возможным отставанием по начальной фазе на некоторый угол j:

q = q_м cos (wt - j)

Задача заключается в отыскании амплитуды q_м и начальной фазы j вынужденных колебаний и в выявлении их зависимости от характеристик вынуждающей ЭДС и собственных характеристик колебательного контура.

Подставив в дифференциальное уравнение вынужденных колебаний заряда первую q¢ и вторую q¢¢ производные от q = q_м cos (wt - j), получим:

w²q_мcos (wt - j) - 2wdq_мsin (wt - j) + w_о²q_мcos (wt - j) = (e_м/L)cos wt.

Приведем все тригонометрические функции к единой - косинусу:

w²q_мcos (wt - j + p) + 2wdq_мcos(wt - j + p/2) + w_о²q_мcos (wt - j) = (e_м/L)cos wt.

Получили тригонометрическое равенство, в котором сумма трех гармонических функций - колебаний одинаковой частоты, приравнивается к четвертой - вынуждающей «силе». Решение такого уравнения удобно провести с помощью векторной диаграммы. На ней гармоническое колеба­ние изображается в виде вектора, модуль (длина) которого равен амплитуде колебания, и который вращается вокруг оси (Х или У) c угловой скоростью, равной частоте w колебания, будучи в началь­ный момент наклоненным к оси под углом, равным начальной фазе колебания. Так как все колеба­ния имеют одинаковую частоту, изображающие их векторы будут вращаться с одинаковой скоро­стью, и их относительная взаимоориентация с течением времени будет оставаться неизменной.

Векторная диаграмма позволяет заменить сло­жение гармонических функций (колебаний) одинаковой час­тоты сложением векторов, что значительно проще и нагляднее. Изобразим на векторной диаграмме связь гармонических функций, даваемую уравнением вынуж­денных колеба­ний.

Из векторной диаграммы выразим искомые началь­ную фазу j и амплитуду q_м вынужденных колебаний заряда в контуре:

tg j = 2wdq_м/[(w_о² - w²)q_м];

Þ j = arctg{2wd/[(w_о² - w²)}

(e_м/L)² = [(w_о² - w²)q_м + (2wdq_м)²

Þ q_м = (e_м/L)/Ö[(w_о² - w²) + 4w²d²]

Полученные выражения показывают, что амплитуда и фаза вынужденных колебаний заряда
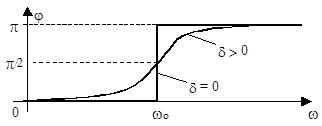
в контуре зависят от коэффициента затухания d и соотношения частот w_о и w (свободных колебаний и вынуждающей силы). Графики зависимостей q_м(w) и j(w), называемые, соответственно, ампли­тудно- и фазочастотными характеристиками (АЧХ и ФЧХ) заряда для разных значений коэффици­ента затухания d, играющего роль параметра в зависимостях q_м(w) и j(w), имеют следующий вид:

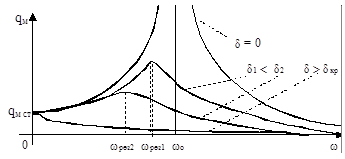
На графике зависимости амплитуды q_м вынужденных колебаний заряда в контуре от частоты w внешнего источника имеет место максимум. Это явление или особенность АЧХ называют резо­нансом. Резонансная частота w_р, соответствующая максимуму q_м, формально определяется из усло­вия экстремума функции q_м(w):

q_м¢(w) = 0 Þ w_р = Ö(w_о² - 2d²) (w_р £ w_о)

Затухание колебаний, его мера - коэффициент d - понижает резонансную частоту w_р и уменьшает резонансную амплитуду q_мр вынужденных колебаний заряда в контуре (с увеличением d максимумы АЧХ понижаются и смещаются в область меньших частот - резонанс «левеет» и «тупеет»).

Резонансную амплитуду q_мр найдем, подставляя в формулу q_м(w) значение резонансной частоты w_р = Ö(w_о² - 2d²):

q_мр = (e_м/2dL)/Ö(w_р² - d²).

В отсутствие затухания (при d = 0) значение резонансной амплитуды q_мр = ¥. Это естествен­ный результат, реакция вынужденных колебаний на вынуждающую силу в отсутствие диссипации, поглощения энергии внешнего источника, которые только и могут ограничить амплитуду вынуж­денных колебаний.

При w = 0 имеем статический случай с внешним источником постоянного тока. На конденса­торе имеет место статический заряд

q_{м о} = q_{м ст} = Сe_м = e_м/w_о²L (w_о² = 1/LC)

При w = ¥ амплитуда вынужденных колебаний заряда равна нулю; вследствие инертности и диссипации колебания не успевают «раскачиваться» с бесконечно высокой частотой, скоростью.

При достаточно большом затухании d > d_кр = w_о/Ö2 резонансная частота становится мнимой; вместо резонансной зависимости (с максимумом) имеет место монотонный спад амплитуды вынуж­денных колебаний заряда при увеличении частоты внешнего источника. Диссипация, то есть необра­тимый перевод в тепло энергии внешнего источника, преобладает здесь над упругостью и инертно­стью.

Анализ фазочастотной характеристики показывает, что вынужденные колебания всегда отстают по фазе от вынуждающей силы (следствие всегда запаздывает от причины). Это отставание-запаздывание увеличивается с ростом затухания в колебательной системе. При нулевом затухании (d = 0) угол j отставания по фазе вынужденных колебаний заряда от внешней ЭДС скачком изменя­ется на p (от 0 до 180°) при w = w_о, то есть на частоте собственных колебаний системы (контура).

На частотах, меньших w_о, колебания заряда в контуре совпадают по фазе с вынуждающей ЭДС, а на частотах, превышающих w_о, заряд колеблется в противофазе с колебаниями внешнего источника.

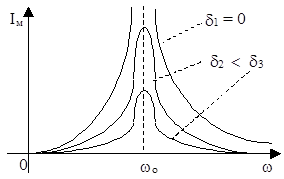
Колебания силы тока I = dq/dt в контуре также носят резонансный характер, то есть зависи­мость их амплитуды I_м от частоты вынуждающей ЭДС имеет максимум. Но в отличие от резонанса заряда, резонанс тока в контуре всегда происходит на одной частоте, равной частоте w_о свободных колебаний в контуре. Формально это связано с тем, что в выражении для амплитуды силы тока I_м = wq_м появля­ется еще один множитель - частота w. Поэтому характер частотной зависимости I_м(w) становится отличным от q_м(w):

I = dq/dt = - wq_мsin (wt - j) = I_мcos (wt - j + p/2),

где I_м = wq_м = (we_м/L)/Ö[(w_о² - w²) + 4w²d²] Þ Þ dI_м/dt = 0 при w = w_о = 1/Ö(LC)

В чем же причины и физический механизм такого специфического эффекта, как резонанс? Почему вынужденные колебания особенно эффективно возбуждаются на определенной частоте вынуждающей силы? Как и в случае механических колебаний причины резонанса электромагнитных колебаний (заряда и тока) кроются в фазовых соотношениях, то есть резонанс является эффектом амплитудно-фазовым. На резонансной частоте вынужденные колебания силы тока, то есть быст­роты, скорости колебаний заряда, оказываются сфазированными с колебаниями внешнего источ­ника, возбуждающего вынужденные колебания в контуре. Колебания же заряда, которые отстают по фазе от колебаний тока на p/2, на резонансной частоте отстают на p/2 и от колебаний внешнего источника.

Именно на резонансной частоте создаются наиболее благоприятные, оптимальные условия для перекачки энергии внешнего источника в контур, для потребления ее на раскачку собственных колебаний в контуре. На резонансной частоте вынуждающая сила в течение всего периода колеба­ний действует в направлении (синфазно, синхронно) скорости (перемещения) вынужденных колеба­ний и совершает максимальную работу по их раскачке, наращиванию их амплитуды. Из механики следует, что источник развивает наибольшую мощность N

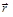N = dА/dt = d/dt = = F u cos j,

когда сила сонаправлена со скоростью перемещаемого тела. В случае гармонического характера воздействия (и отклика) эта сонаправленность выражается в сфазированности (синфазности) во времени вынуждающей силы и скорости вынужденных колебаний.

На частотах, как меньших, так и больших резонансной, то есть при w ¹ w_р, сфазированность внешнего источника и вынужденных колебаний нарушается. При этом лишь часть периода внешний источник совершает положительную работу по раскачке вынужденных колебаний в контуре; в тече­ние же другой части эта работа оказывается отрицательной, тормозящей вынужденные колебания.

При w ® ¥ отставание вынужденных колебаний по фазе от вынуждающей силы достигает 180°, и положительная работа внешнего источника сравнивается с его отрицательной работой, результатом чего является стремление амплитуды вынужденных колебаний к нулю (вынужденные колебания не возбуждаются).

Дата добавления: 2014-01-06