Методи дослідження стійкості нелінійних систем

Єдиним методом точного дослідження стійкості НЛС є метод фазових траєкторій, однак він обмежується системами другого порядку. В сучасних умовах при дослідженні стійкості НЛС доцільно орієнтуватись на застосування комп’ютерного моделювання.

Основоположними роботами в галузі стійкості НЛС є дослідження російського вченого Ляпунова О.М., які складають основу загальної теорії стійкості. Крім того, використовуються критерії абсолютної стійкості В.М.Попова, метод гармонійної лінеаризації для дослідження автоколивань і інш.

В загальній постановці дослідження стійкості НЛС використовуються методи:

- визначення достатніх умов стійкості на основі критеріїв, які дозволяють виділити частину повної області стійкості;

- наближеного дослідження.

В першому випадку наперед відомий знак похибки у визначенні межі стійкості, а сама похибка відноситься до запасу стійкості, хоча її величина невідома і може бути як завгодно великою. У другому випадку знак похибки невідомий, але є можливість оцінити зверху її абсолютну величину.

О.М. Ляпунов в 1892 році дав визначення, яке до цього часу є загально визнаним, класичним і складає основу теорії стійкості нелінійних систем (в технічній літературі - стійкість по Ляпунову):

Незбурений рух є стійким, якщо при достатньо малих початкових збуреннях викликаний ним збурений рух як завгодно мало відрізняється від незбуреного; при цьому рух асимптотично стійкий, якщо при 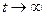збурений рух прямує до незбуреного.

В такій постановці незбурений рух – будь-який режим роботи системи щодо стійкості. У фазовому просторі – це початок координат, а в загальному випадку цим режимом може бути як усталений статичний чи динамічний режими, так і неусталений режим. Як збурення Ляпунов розглядав лише ненульові початкові умови, які відповідають початковому зміщенню зображаючої точки з початку координат в певну точку фазового простору при незмінних зовнішніх діяннях, які відповідають незбуреному рухові. З практичної точки зору це незручне визначення збурення, але при достатньо загальних умовах режим, асимптотично стійкий за Ляпуновим, буде стійким при розгляді збурення, яке відповідає відхиленню зовнішніх діянь.

Рис. 1.14. Оцінка стану рівноваги НЛС

Графічна інтерпретація стійкості за Ляпуновим показана на рис 1.14: стан рівноваги стійкий, якщо для будь-якої заданої області допустимих відхилень ε можна вказати таку допоміжну область η (ε), щоб жодний рух, який починається в цій області, не досягав межі ε. Це значить, що при заданій області допустимих відхилень ε визначається область початкових умов η. При цьому для стійкої системи не обов’язково вимагати повернення до попереднього стану рівноваги, а достатньо, щоб рух зображаючої точки відбувався в межах області допустимих відхилень ε. Якщо ж система не тільки не виходить за межі допустимої області, а повертається до попереднього стану рівноваги, то таку систему називають асимптотично стійкою. Стійкість рівноваги за Лапуновим гарантує стійкість “в малому”, але система може бути нестійкою “у великому” (рис. 1.15).

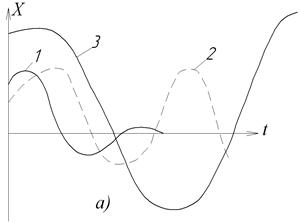
Рис.1.15. До оцінки стійкості НЛС

а) перехідні процеси; б) фазові траєкторії

Перехідним процесам 1,2,3 відповідають фазові траєкторії 1’, 2’,3’.

Ляпуновим О.М. розроблено два методи дослідження стійкості НЛС. Перший метод використовується лише для дослідження стійкості “в малому” тих систем, які можна лінеаризувати шляхом розкладання функцій нелінійності в ряд Тейлора. Цим самим вперше було доведено, що стійкість нелінійної системи можна оцінювати за стійкістю лінеаризованої системи. Перший метод Ляпунова включає кілька теорем, головними висновками яких є:

- якщо лінійна система першого наближення (лінеаризована система) стійка, то стійкою є і вихідна (досліджувана) нелінійна система;

- якщо лінеаризоване система нестійка, то нестійка і досліджувана нелінійна система;

- якщо лінеаризоване система знаходиться на межі стійкості, то зробити висновок щодо стійкості нелінійної системи неможливо (вона може бути як стійкою, так і нестійкою).

Перших два висновки дають можливість застосувати при дослідження нелінійної системи методи теорії лінійних систем, що значно спрощує проблему. При цьому необхідно враховувати, що перший метод Ляпунова застосовується для дослідження стійкості “в малому”. Третій висновок привів до необхідності розробки спеціального метода, який отримав назву прямого метода дослідження стійкості НЛС,

Другий метод Ляпунова О.М. є найбільш загальним і дозволяє визначити достатні умови стійкості, тобто виділити частину загальної області стійкості.

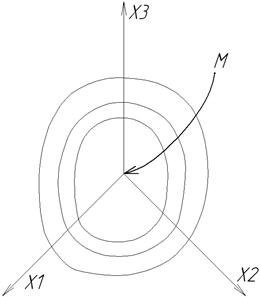
Рис. 1.16. До прямого метода Ляпунова О.М.

Головну ідею метода зручно пояснити, використовуючи фазовий простір (рис.1.16). Розглядається замкнена поверхня довільної форми, яка описується рівнянням:

(1.28)

де: - функція координат системи х₁, х₂...х_n;

C - параметр, який визначає величину функції.

Кожному значенню С відповідає певна поверхня у фазовому просторі. При зменшенні С поверхня стискується так, що при 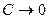поверхня стягується в початок координат. Тоді достатньою умовою стійкості системи буде необхідність руху точки М лише в середину поверхні, тобто в напрямку зменшення С. Це означає, що вздовж фазових траєкторій похідна 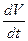буде від’ємною.

Таким чином, достатні умови стійкості за Ляпуновим формулюються так: якщо для нелінійної системи можна підібрати таку знаковизначену функцію 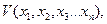щоб її похідна 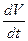, взята вздовж фазової траєкторії, також була знаковизначеною (або знакопостійною), але мала знак, протилежний знаку V, то система стійка, причому при знаковизначеній функції 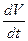- асимптотично стійка.

Знаковизначена функція у всіх точках області в околі початку координат зберігає знак і не дорівнює нулю, крім початку координат, наприклад:

Знакостійна функція не змінює знак, але може обертатись в нуль не лише на початку координат, наприклад:

Знакозмінна функція змінює знак в околі початку координат, наприклад

є додатньою для точок зправа від прямої х₁= -х₂ та від’ємною –зліва від прямої.

Труднощі використання прямого метода Ляпунова пов’язані з відсутністю загальних правил формування функцій V. Варто підкреслити, що функція Ляпунова – це не конкретна функція, а така, яка задовольняє умовам задачі. Крім того, поза межами області стійкості, визначеними функціями V, нічого не можна сказати про стійкість, тобто не відомо, яка частина повної області стійкості знайдена.

При дослідженні стійкості нелінійних систем використовується також критерій абсолютної стійкості В.М.Попова, коли нелінійність задається не конкретним видом, а належністю до певного класу. Статичні характеристики (рис.1.17) вважаються одного класу, якщо вони розташовані в секторі, обмеженому прямою з кутовим коефіцієнтом k_н. Така постановка задачі з математичної точки зору дозволяє значно спростити дослідження системи, а також має практичне значення, коли нелінійності задані неточно або змінюються в процесі роботи.

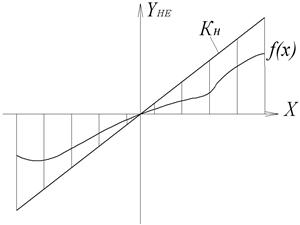
Рис.1.17. Клас нелінійних характеристик

Критерій В.М.Попова відноситься до частотних, для чого записується частотна характеристика лінійної частини:

(1.29)

З виразу (1.29) отримують модифіковану частотну характеристику:

(1.30)

де: T_m – нормуючий множник, 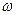- поточна частота; T_m=1с.

Для нелінійної системи, яка складається з лінійної частини з АФХ і нелінійного елемента з характеристикою f(x), розташованою в секторі [0, k_н], критерій абсолютної стійкості формується так:

для абсолютної стійкості рівноваги достатньо, щоб модифіково-частотна характеристика не охоплювала точку (-1/ k_н;0) і через цю точку можна було провести пряму, яка не перетинає характеристику .

Рис.1.18. Критерій абсолютної стійкості В.М.Попова

На рис.1.18 показані випадки: а) система стійка; б,в) нестійка.

За допомогою критерія В.М.Попова вирішується і обернена задача: будується задана характеристика , потім проводиться якомога ближче до неї пряма так, щоб отримати найменший відрізок [0;-1/ k_н] і таким чином знаходять допустиме значення кутового коефіцієнта k_н. За нахилом прямої, “притиснутої” до кривої , можна зробити висновок щодо допустимого класу нелінійності: якщо пряма вертикальна, то нелінійність може бути лише однозначною, а якщо нахилена – може бути довільною, в тому числі із гістерезисом.

1.7. Методи дослідження режимів роботи та якості нелінійних систем

Вище зазначалось, що однією з особливостей нелінійних систем є виникнення автоколивань, які на відміну від лінійних систем є робочим режимом і можуть підтримуватись як завгодно довго, наприклад, в нелінійних системах з релейним елементом. Таким чином, автоколивання є внутрішньою (власною) властивістю системи, тому виникає задача визначення частоти та амплітуди автоколивань, що дає можливість оцінити їх якість.

Одним з методів дослідження автоколивань є метод гармонійного балансу, заснований на методі гармонійної лінеаризації. Наприклад, коли розглядаються автоколивання у вигляді:

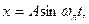(1.31)

тобто без постійної складової, тобто для нелінійної ланки з непарною характеристикою і без зовнішнього збурення, яке спричиняє х₀. То після гармонійної лінеаризації можна отримати лінійну ланку для якої

(1.32)

Значення W_нл(р) залежить від коефіцієнтів гармонійної лінеаризації, які в свою чергу залежать від амплітуди А та частоти 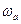автоколивань, тобто . Для типових нелінійностей існують готові формули для коефіцієнтів.

Для розімкненої системи з нелінійністю можна записати вираз:

(1.33)

тобто цим підкреслюється, що передаточна функція нелінійного елемента залежить від амплітуди х_нmax та частоти . При постійній амплітуді х_нmax=А=const та частоті ==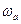const для системи, яка описується виразом (1.33), можна застосувати методи лінійної теорії керування. Для лінеаризованої системи існування автоколивань відповідає знаходження її на межі стійкості, тому для дослідження автоколивань зручно використовувати частотні критерії Найквіста та Михайлова. За критерієм Найквіста умовою знаходження системи на межі стійкості є:

(1.34)

звідки:

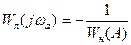(1.35)

Рівняння (1.35) зручно розв’язувати графічно (рис.1.19), де визначаються точки перетину годографів і . Ці точки свідчать про існування автоколивань, крім того з в точці М₁ або М₂ визначається частота, а з - амплітуда автоколивань. За графіками, показаними на рис.1.19, можна зробити також висновок щодо стійкості автоколивань: в т.М₂ – стійкі, в т.М₁ – нестійкі.

Рис.1.19. Визначення параметрів автоколивань

Аналіз властивостей НЛС, зокрема параметрів автоколивань, здійснюється також за допомогою точкових перетворень (рис.1.20).

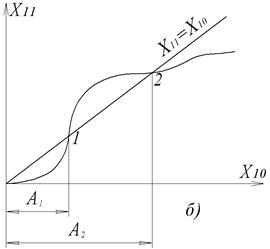
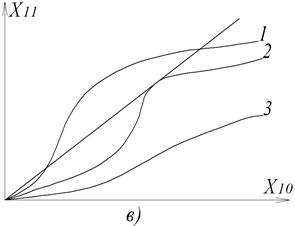
Рис.1.20. Метод точкових перетворень

Початкове положення зображаючої точки М₀ обирається на додатній півосі х₁. Після одного оберту точка може попасти в різні місця. Знаходять функцію х₁₁=f(x₁₀), тоді можна зробити висновки: при х₁₁<x₁₀ – процес збіжний, при х₁₁=x₁₀ – граничний цикл (автоколивання), х₁₁>x₁₀ – розбіжний процес. На рис.1.20,б розбіжний процес відповідає відрізкові між т.1 і т.2. Різні стани НЛС демонструє рис.1.20,в: 1- відповідає рис.1.20,б; 2 – в НЛС можливі автоколивання; 3 – НЛС стійка в цілому.

При дослідженні стаціонарних режимів НЛС під дією детермінованих сигналів зберігаються основні положення, отримані для лінійних систем: вплив коефіцієнтів передачі, порядку астатизму, компенсації зовнішніх збурень. В той же час необхідно врахувати наявність нелінійних статичних характеристик (рис.1.21): 1 – з гістерезисом, 2 – з зоною нечутливості.

Рис.1.21. Нелінійні статичні характеристики

Наближеною оцінкою точності НЛС є відношення

(1.36)

яке характеризує статизм системи, причому це відношення змінне.

Рис.1.22. Вплив зворотніх зв’язків на характеристики НЛС

Застосовуючи різні зворотні зв’язки, можна змінювати властивості системи. На рис.1.22,а показана схема із зустрічно-паралельним з’єднанням елементів, причому зворотній зв’язок може бути як додатнім, так і від’ємним. На рис.1.22,б показані статичні характеристики: 1 – ланки 1: х=f; 2 – ланки 2: х_зз=f₂(x). З урахуванням залежностей:

(1.37)

(1.38)

будуються характеристики системи: 3 – при від’ємному зворотньому зв’язку, 4 – при додатному. В результаті отримують висновки: від’ємний зворотній зв’язок зменшує крутизну результуючої характеристики, а додатній – збільшує. Це ж стосується нелінійностей.

Для оцінки точності статичного режиму НЛС використовується такий метод: для замкненої системи “об’єкт-пристрій управління” (рис.1.23,а) будують статичні характеристики X=f₁(U) при різних

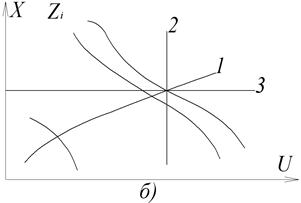
Рис.1.23. Оцінка статичного режиму НЛС

значеннях збурення Z_i (рис.1.23,б). На ці характеристики наносять статичні характеристики пристрою управління U=f₂(X). Точки перетину дають можливість побудувати результуючу характеристику Х=f₃(Z), за якою можна визначити оцінку 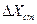при 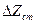. Криві 2 та 2’ характеризують відсутність керування. При збільшенні коефіцієнта передачі ПУ та введені інтегруючої ланки система стає астатичною (криві 3; 3’). Криві 1,1’ характеризують проміжний режим роботи системи. Можна побудувати також статичні характеристики системи відносно . В результаті отримують оцінки впливу нелінійностей та нестабільності окремих ланок на властивості системи, що дає можливість взаємно узгодити характеристики окремих частин системи.

Для оцінки точності НЛС при дії випадкових сигналів передбачається, що зовнішній сигнал є стаціонарним:

(1.39)

і високочастотна складова 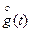характеризується відомою оцінкою спектральної щільності 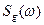. Під впливом цього збурення виникає випадковий сигнал похибки:

(1.40)

Застосовуючи метод статистичної лінеаризації, отримують оцінки:

(1.41)

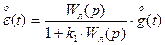(1.42)

Постійну складову сигналу похибки визначають, застосовуючи теорему про кінцеве значення оригіналу в перетворенні Лапласа

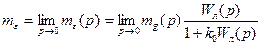(1.43)

Випадкову складову сигналу похибки характеризує оцінка дисперсії:

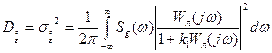(1.44)

В праву частину рівнянь (1.43), (1.44) входять коефіцієнти статистичної лінеаризації k₀ і k₁, які в свою чергу залежать від оцінок m_g і :

(1.45)

(1.46)

Останні чотири рівняння (1.43) – (1.46) розв’язують спільно, наприклад, методом послідовних наближень. Якщо в системі виникають автоколивання, то необхідно використовувати спільно методи статистичної і гармонійної лінеаризації.

Якість перехідних процесів НЛС оцінюється такими ж показниками, як і для лінійних систем (динамічна та статична похибка, тривалість перехідного процесу, коливальність і інш.), але при цьому необхідно насамперед враховувати величину зовнішнього сигналу. Найбільш ефективним методом дослідження якості НЛС є використання комп’ютерних технологій.

[1, с.3-30, 2, c.311-359]

Контрольні запитання.

1. Які системи називають нелінійними і які їх особливості?

2. Що таке типові нелінійності і за якими ознаками їх класифікують?

3. В чому полягають особливості проходження гармонійного сигналу через нелінійну систему?

4. В яких координатах будуються фазові траекторії нелінійних систем?

5. Які особливості точки фазових траекторій і існують в нелінійних системах?

6. Наведіть приклад відповідності перехідних процесів і фазових траекторій.

7. Які особливості мають фазові траекторії нелінійних систем?

8. За яких умов в нелінійних системах можуть виникати і підтримуватись автоколивання?

9. Наведіть приклад проходження випадкового сигналу через нелінійну систему.

10. На яких залежностях будується метод статистичної лінеарізації?

11. Як визначаються коефіцієнти статистичної лінеарізації?

12. Охарактеризуйте процедуру гармонійної лінеарізації.

13. Поясніть принцип та ефект вібраційної лінеарізації.

14. Сформулюйте загальну постановку проблеми дослідження стійкості ща Ляпуновим О.М.

15. В чому полягає зміст першого та другого методів Ляпунова О.М.дослідження стійкості нелінійних систем?

16. Як формулюється критерій абсолютної стійкості?

17. Як досліджуються автоколивання в нелінійних системах?

18. Як оцінюється точність нелінійної системи в статичному режимі при детермінованих чи випадкових ділянках?

Дата добавления: 2014-01-06