Лінійні імпульсні системи

3.2.1. Загальна характеристика імпульсних систем (ІС)

Процес квантування неперервного сигналу за часом – імпульсна модуляція, тобто перетворення неперервного вхідного сигналу в послідовність, наприклад, амплітудно – модульованих імпульсів з обвідною, яка співпадає з вхідним сигналом. Вихідний сигнал імпульсного елемента (рис.3.2) характеризується кількома основними параметрами:

А – амплітуда;

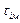- тривалість (ширина) імпульсу;

Т_п – період повторення імпульсів; Т_п - 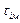- пауза;

- шпарність імпульсу.

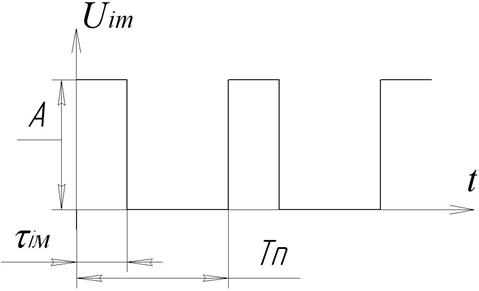
Рис.3.2 Вихідний сигнал імпульсного елемента

Імпульсна модуляція – змінювання одного з параметрів вихідних імпульсів (модулюємого) у функції величини вхідного сигналу (модулюючого). Може змінюватись (модулюватись) амплітуда, ширина імпульсу, пауза. Відповідно виділяють види імпульсної модуляції:

- амплітудно-імпульсна (АІМ) – рис.3.2, а;

- широтно-імпульсна (ШІМ) – рис.3.2, б;

- часо-імпульсна (ЧІМ) - рис. 3.2, в.

На рис. 3.2 х – вхідний сигнал імпульсного елемента (ІЕ).

Рис.3.2. Види імпульсної модуляції

При АІМ змінюється амплітуда A=f(х),

При ШІМ: 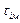=f(х), A, T_n – const.

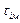При ЧІМ (різновид – фазоімпульсна модуляція):=f(х), A,, T_n – const.

В задачах аналізу та синтезу імпульсні системи (ІС) подають у вигляді двох частин – імпульсного елемента ІЕ і неперервної частини НЧ (рис.3.3).

Рис.3.3. Структура імпульсної системи

Якщо частота імпульсів на виході ІЕ значно більша смуги пропускання НЧ, то ІС можна розглядати як неперервну, тобто квантування за часом не викликає значних особливостей в роботі системи. Неперервна частина НЧ – фільтр нижніх частот, тому у випадку з АІМ вона реагує лише на низькочастотну складову сигналу U_IE, але дискретність роботи ІЕ формує на виході НЧ високочастотну складову у вигляді фону, частотний спектр якої кратний частоті роботи ІЕ (рис.3.4).

Рис. 3.4 Сигнали в імпульсній системі

При недостатньо високій частоті роботи ІЕ в порівнянні із смугою пропускання НЧ системи виникають суттєві відмінності від функціонування неперервної системи.

Імпульсну систему можна замінити неперервною при виконанні таких умов:

(3.1)

де: - частота повторення імпульсів;

- смуга пропускання частот неперервної частини;

- спектр (найбільша частота) зовнішнього сигналу, приведеного до входу ІЕ.

При виконанні першої нерівності частотні характеристики неперервної та імпульсної систем в межах смуги пропускання неперервної частини співпадають. Бокові частоти, які є на виході імпульсного елемента, не проходять на вихід низькочастотної частини, тобто ІС буде реагувати на низькочастотні зовнішні сигнали так, як і неперервна система. Друга нерівність обмежує частоту зовнішнього сигналу так, щоб його частотний спектр після проходження через ІЕ 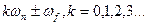був у межах і не відрізнявся від частотного спектра при відсутності ІЕ. При невиконанні другої нерівності на виході ІС з’являються низькочастотні складові, яких немає в неперервній системі.

Виконання умов (3.1) дає можливість не враховувати квантування за часом і розглядати ІС як неперервну. Ці умови фактично є наслідком теореми Котельникова – Шеннона про умови неспотвореної передачі неперервного сигналу кінцевим числом його дискретних значень, що справедливо для систем з АІМ.

Дата добавления: 2014-01-06