Функціональна та алгоритмічна структури ІС з АІМ

Імпульсний елемент може входити до складу будь-якого блока системи, наприклад, датчика, але в більшості випадків в ІС є спеціальні пристрої (комутатори), які періодично замикають та розривають ланцюг регулювання.

В задачах аналізу ІС приводять до структури, зображеної на рис.3.5.

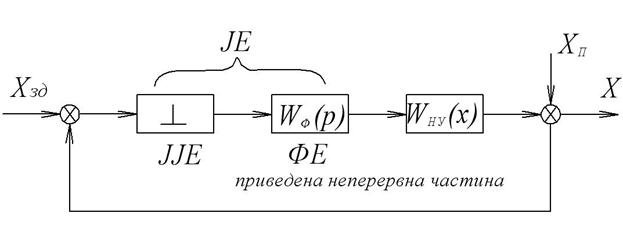
Рис.3.5. Алгоритмічна структура ІС

Реальний імпульсний елемент ІЕ розкладається на ідеальний імпульсний елемент ІІЕ і формуючий елемент ФЕ, який разом з неперервною частиною системи утворюють так звану приведену неперервну частину системи. Ідеальний імпульсний елемент ІІЕ перетворює неперервний сигнал у послідовність миттєвих імпульсів, які рівновіддалені один від одного та мають площі, які дорівнюють значенням вхідного сигналу в дискретні моменти часу, тобто формується 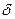- функція. Формуючий елемент (демодулятор) утворює з миттєвих імпульсів такі, які за формою співпадають з імпульсами на виході реального ІЕ. Реакція формуючого елемента ФЕ на одиничний імпульс, тобто 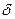- функцію – це вагова функція w_ф(t), звідки передаточна функція ФЕ буде:

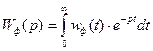(3.2)

Фактично w_ф(t) = w_ім (t) – функція, яка описує імпульс на виході реального ІЕ при дії на вході 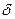- функції.

Формуючий елемент ФЕ можна розглядати як ланку неперервної дії, тоді передаточна функція приведеної неперервної частини буде:

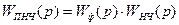(3.3)

В більшості випадків імпульси на виході ІЕ мають прямокутну форму, тоді ФЕ повинен перетворювати одиничну 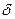- функцію в прямокутний імпульс одиничної висоти і тривалості 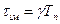(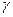- шпарність). Такий імпульс можна подати у вигляді різниці двох ступінчастих функцій зі зсувом на час :

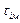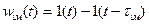(3.4)

Тоді передаточна функція формуючого елемента ФЕ буде:

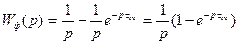(3.5)

Якщо тривалість імпульсів 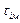суттєво менша основних постійних часу неперервної частини системи, то ФЕ можна наближено замінити без інерційною ланкою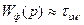

При 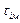=Т_п ФЕ видає постійний сигнал, який дорівнює значенню вхідного сигналу на початку періоду Т_п. В цьому розповсюдженому випадку ФЕ називають фіксуючим (запам’ятовуючим), тоді:

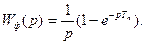(3.6)

Такий ФЕ називають екстраполятором нульового порядку.

Для імпульсних систем частота квантування має важливе значення. Наслідком теореми про квантування (теореми Котельникова - Шеннона) є твердження: якщо неперервний сигнал має спектр, обмежений частотою 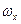, то його квантування за часом з частотою 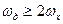не приводить до втрати інформації, тобто сигнал однозначно і точно передається своїми дискретними значеннями, взятими через інтервал квантування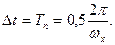

При достатньо великій частоті повторення 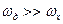фіксатор (3.6) за своїми властивостями наближається до ланки запізнювання:

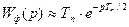(3.7)

В цьому випадку ІС може розглядатись як неперервна, але запас її стійкості зменшується.

Фіксатор (3.6) можна описувати наближено передаточною функцією аперіодичної ланки:

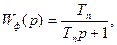(3.8)

що справедливо при високій частоті квантування.

Для практичних розрахунків частоту квантування приймають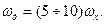

Дата добавления: 2014-01-06