Цифрові системи

В цифрових системах відбувається квантування сигналів за часом і рівнем. Квантування за часом робить цифрову систему дискретною, а квантування за рівнем – нелінійною. В цифрових системах є пристрої, які перетворюють неперервні сигнали в цифрові коди і виконують математичні операції над цими кодами. Цифровий регулятор виконує властиві йому операції і видає результати у дискретні моменти часу t = T_n, 2T_n, 3T_n… В інтервалах між цими моментами на виході регулятора зберігається певний сигнал, тобто вихідний сигнал – ступінчаста функція x(iT_n), яка відповідає квантуванню за часом. Квантування за рівнем обумовлюється тим, що внаслідок цифрової подачі інформації вихідний сигнал може набувати лише певних фіксованих рівнів, які відрізняються один від одного на величину q. Ця величина відповідає одиниці молодшого розряду цифрового регулятора, тобто неперервний сигнал подається у виді:

(3.51)

де: а х^*(іТ_п) містить ціле число рівнів q. При малих q впливом квантування за рівнем на динаміку систем можна знехтувати, тобто покласти У загальному випадку для дослідження цифрових систем можна застосувати математичний апарат, який використовується для лінійних імпульсних систем з амплітудно - імпульсною модуляцією: Z – перетворення і різницеві рівняння.

В системах автоматичного керування технологічними об’єктами функції регулятора виконує мікропроцесорний контролер. Така система відноситься до неперервно – дискретних і описується диференціальними і різницевими рівняннями, а також включає функціональні залежності, які відображають перетворення сигналів з неперервної форми в дискретну і навпаки. Така структура математичного опису громіздка і незручна.

Більш зручним методом є заміна диференціальних рівнянь різницевими, тоді в цілому аналіз і синтез систем виконується методами теорії неперервних систем, а синтезований регулятор реалізується в цифровому виді. При цьому необхідно врахувати, що при названих замінах виникають похибки, які можуть привести до різних оцінок, наприклад, щодо стійкості.

Узагальнена функціональна структура цифрової системи показана на рис.3.12.

Рис.3.12 Функціональна структура цифрової системи керування

Об’єкт керування ОК – неперервна частина системи (НЧ). Аналогово – цифровий перетворювач АЦП призначений для отримання з неперервного сигналу цифрового коду, який обробляється в ЕОМ або мікропроцесорному контролері МПК. Для формування сигналу керування U, який поступає на об’єкт, необхідно забезпечити зворотнє перетворення, для чого призначений цифро – аналоговий перетворювач ЦАП. Перетворювач АЦП включає імпульсний елемент для квантування за часом і квантуватель за рівнем. В результаті отримують число у вигляді коду, як правило, двійкового, яке подається в ЕОМ (МПК). Після перетворення за певними алгоритмами результат видається у вигляді чисел U_ц(іТ_п). Перетворювач ЦАП складається з квантувателя за рівнем, ідеального 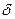- імпульсного елемента і формуючого елемента (екстраполятора). Крім екстраполяторів нульового порядку, які утримують сигнал на постійному рівні між сусідніми імпульсами, застосовуються також екстраполятори першого порядку, сигнал яких змінюється за лінійним законом, і другого – за квадратичною параболою.

Число рівнів квантування вхідного і вихідного сигналів різне: на вході необхідно забезпечити точність обробки сигналів, і число рівнів вхідного сигналу визначається розрядністю ЕОМ (МПК). Вихідний сигнал може мати мінімальну кількість рівнів, тобто сигнал може бути релейним.

В порівнянні з аналоговими (неперервними) системами цифрові системи керування мають ряд особливостей, які визначають їх динаміку:

- квантування сигналів за часом і рівнем;

- цифро – аналогове і аналого – цифрове перетворення. В сучасних системах можна забезпечити необхідну точність цих перетворень, але необхідно врахувати, що в алгоритмах керування використовуються прирости вхідних та вихідних сигналів. Це потребує узгодження розрядності технічних засобів, швидкодії, періоду опитування датчиків і інш.;

- часовий зсув між вхідним сигналом і видачею сигналів керування, тобто наявність запізнювання. Це має особливе значення, коли здійснюється багатооб’єктне керування, виконується множина необхідних алгоритмів.

[1, с.50-70, 2, с.406-453]

Контрольні запитання:

1. Наведіть класифікацію дискретних систем.

2. Релейні (позиційні) системи, їх властивості та область застосування.

3. Якими показниками характеризуються перехідні процеси в релейних системах і від чого вони залежать?

4. Наведіть види імпульсної модуляції.

5. Як впливає частота імпульсів на характеристики системи?

6. За яких умов імпульсну систему можна розглядати як неперервну?

7. В чому полягає призначення фіксуючого елемента (екстраполятора) і як визначається його передаточна функція?

8. Як використовуються решітчасті функції в математичному описі імпульсних систем?

9. Наведіть приклад зв’язку звичайної і дискретної (в Z - перетвореннях) передаточних функцій.

10. Охарактеризуйте сигнали в типовому імпульсному ланцюзі.

11. В чому особливості частотних характеристик імпульсних систем?

12. Як оцінюється стійкість імпульсних систем?

13. В чому особливості застосування критеріїв стійкості імпульсних систем?

14. Як оцінюється якість імпульсних систем?

15. Цифрові системи, їх особливості.

16. В чому особливості динаміки цифрових систем?

17. Як записуються передаточні функції цифрових регуляторів?

Дата добавления: 2014-01-06