Работа с матрицами в MathCAD

Рассмотрим простейшие операции матричной алгебры, реализованные в MathCAD в виде операторов, причем следует отметить, что их запись максимально приближена к математической форме записи. Наиболее часто используемые операции расположены на панели инструментов Матрица (Matrix) (рис. 14), остальные можно найти используя меню Вставка → Функция … категории функций Vector and Matrix.

Рис. 14. Панели инструментов Матрица и Логика

Транспонированием называют операцию, переводящую матрицу размерности M × N в матрицу размерности N × M, делая столбцы исходной матрицы строками, а строки - столбцами. Ввод символа транспонирования (transpose) 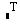осуществляется с помощью панели инструментов Матрица (Matrix) 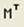или нажатием клавиш <Ctrl>+<1>. Не забывайте, что для вставки символа транспонирования матица должна находиться между линиями ввода.

Сложение и вычитание. В MathCAD можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются стандартные символы «+» или «-», соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых. Результат унарной операции смены знака матрицы эквивалентен смене знака всех ее элементов. Для того, чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом.

При умножении следует помнить, что матрицу размерности M × N допустимо умножать только на матрицу размерности N × P (P может быть любым). В результате получается матрица размерности M × P.

Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Матрица (Matrix), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой.

Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции:

· rows (A) - число строк;

· cols (A) - число столбцов;

· length(v) - число элементов вектора;

· last (v) - индекс последнего элемента вектора,

где A - матрица или вектор; v - вектор.

Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно 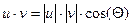, где 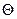- угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение.

Векторное произведение (cross product) двух векторов u и v с углом 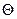между ними равно вектору с модулем 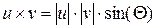, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом <x>, который можно ввести нажатием кнопки Cross Product (Векторное произведение) 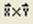в панели Матрица (Matrix) или сочетанием клавиш <Ctrl>+<8>.

Определитель матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Матрица (Matrix) 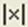или набрать на клавиатуре < | > (нажав клавиши <Shift>+<\>).

Рангом (rank) матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k -го порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы. Для определения ранга матрицы в MathCAD используется функция rank(A), где А - матрица, ранг которой требуется найти.

Как известно, поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Инверсия (Inverse) 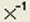на панели инструментов Матрица (Matrix).

В линейной алгебре используются различные векторные и матричные нормы (norm), которые ставят в соответствие матрице некоторую скалярную числовую характеристику. Норма матрицы отражает порядок величины матричных элементов. В разных специфических задачах линейной алгебры применяются различные виды норм. MathCAD имеет четыре встроенных функции для расчета разных норм квадратных матриц:

· norm1(A) - норма в пространстве L1;

· norm2 (А) - норма в пространстве L2;

· norme (A) - евклидова норма (euclidean norm);

· normi (A) — max-норма, или 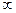-норма (infinity norm):

где A - квадратная матрица.

Часто бывает нужно переставить элементы матрицы или вектора, расположив их в определенной строке или столбце в порядке возрастания или убывания. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц:

· sort(v) - сортировка элементов вектора в порядке возрастания;

· reverse (v) - перестановка элементов вектора в обратном порядке;

· csort(A, i) - сортировка строк матрицы выстраиванием элементов i-столбца в порядке возрастания;

· rsort(A,i) - сортировка столбцов матрицы выстраиванием элементе i-й строки в порядке возрастания, где v - вектор; А - матрица; i - индекс строки или столбца.

Примеры работы рассмотренных выше операторов представлены на рис. 15.

Для задания логических функций в MathCAD имеется панель инструментов Логические (Boolean) рис. 6.13. На ней расположены кнопки, отражающие отношения (=, >, <, £, ³, ¹) и основные логические операции: конъюнкция , дизъюнкция , отрицание 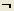и исключающее или (XOR) . Как известно, все логические функции можно выразить через три основные: конъюнкция, дизъюнкция и отрицание, что и отражено в листинге MathCAD-программы на рис. 16. Также в MathCAD можно производить интерпретацию и сложных логических функций (рис. 16).

Рис. 15. Работа с матрицами в MathCAD

Рис. 16. Логические функции в MathCAD

Дата добавления: 2014-01-06