Дифференцирование степенных рядов

Непрерывность суммы степенного ряда. Интегрирование и

Теорема 2. Пусть отрезок 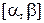лежит в интервале сходимости степенного ряда

,

тогда в 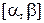этот ряд сходится абсолютно и равномерно.

Доказательство. Пусть для определенности .

Для этот ряд сходится. Далее повторяем доказательства а) теоремы Абеля для .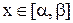

Перенесем теперь рассмотренные выше свойства равномерно сходящихся рядов на случай степенных рядов.

Свойства степенных рядов.

1) Сумма степенного ряда (10.17) 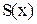непрерывна в интервале сходимости .

Это следует из того, что любое можно заключить в отрезок 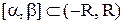, в котором ряд (10.17) сходится равномерно.

2) Пусть 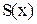-сумма степенного ряда (10.17) и отрезок лежит в интервале сходимости , тогда

.

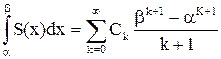Здесь в правой части равенства стоит сумма интегралов членов ряда (3)

.

3) Производная суммы 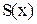степенного ряда (3) в интервале сходимости равна сумме степенного ряда, составленного из производных членов ряда (3), т.е.

.

Здесь мы оставили без доказательства тот факт, что ряд из производных ряда (3) имеет тот же интервал сходимости .

4) Сумма степенного ряда (3) в интервале бесконечно дифференцируема.

Это следует из того, что согласно свойству 3) 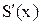является суммой степенного ряда, поэтому операцию дифференцирования можно провести еще один раз, 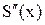снова является суммой степенного ряда в и т.д.

Определение. Функциональный ряд

(7)

называется смещенным степенным рядом с центром в .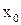

Если обозначить через 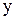, то смещенный степенной ряд превращается в степенной ряд вида (3). Поэтому ряд (7) имеет интервал сходимости вида и в этом интервале обладает всеми свойствами степенных рядов.

Примеры из экономики. В экономике бесконечные ряды и их суммы появляются в основном в теоретических исследованиях. Предположим, рассматривается вопрос о рыночной цене бессрочной облигации номиналом 1000$. И 3-процентным купоном. Это значит, что владелец этой облигации будет каждый год получать 30$. Но как определить истинную цену всей этой бесконечной последовательности платежей? Как правило, любая валюта подвержена инфляции небольшая инфляция 1-2% полезна). Если инфляция составляет 2% в год, то 30$, которые получим через год, сейчас эквивалентны 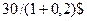, через 2 года - и т.д. Выходит, что бесконечный ряд платежей эквивалентны сумме ряда .

Такого рода дисконтирование, т.е. нахождение сегодняшних эквивалентов прошлых и будущих платежей, применяется и в других ситуациях. Для выяснения, какая лучше из двух стратегий фирмы будет в будущем. Сегодняшний эквивалент этих дисконтированных прибылей представляет сумму бесконечного ряда. Какая их этих сумм больше, ту стратегию, наверное, и нужно выбирать.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М.:Наука, 1988г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.:Наука, 1985г.

3. Кудрявцев Л.Д. Курс математического анализа. Т. 1,2, М.: Высшая школа, 1981г.

4. Бронштейн И.Н.,Семендяев К.А. Справочник по математике для инженеров.М.: Высшая школа,1997.

5. ИДЗ. Дифференциальное исчисление функции одной переменной. Под редакцией Рябушко А.П., ч.1,2 Минск, «ВШ», 2002г.

Дата добавления: 2014-01-06