Степенные ряды. Интервал сходимости

Степенные ряды, т.е. ряды, члены которых есть степенные функции, являются одним из основных примеров функциональных рядов.

Определение. Ряд вида

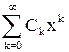(3)

называется степенным рядом, а числа 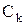называются его коэффициентами.

Степенной ряд всегда сходится при 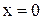. Следующая теорема описывает его область сходимости.

Теорема 1. (Теорема Абеля)

а) Если степенной ряд (3) сходится в точке 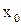(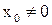), то он сходится для всех 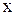из интервала 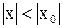(см. рис.1,а)).

б) Если степенной ряд расходится в точке 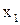, то он расходится для всех 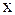, удовлетворяющих неравенству 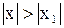(см. рис.1,б)).

Рис. 1, а).

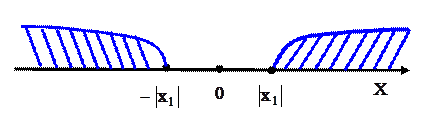
Рис.1, б)

Доказательство. а) Так как ряд

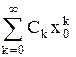
сходится, то согласно необходимому признаку 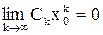, откуда следует, что последовательность 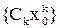ограничена, т.е. существует число 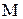, такое что

.

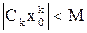Пусть 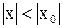. Рассмотрим абсолютную сходимость ряда

.

Получим

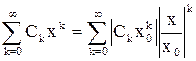. (4)

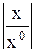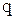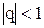Обозначим через , где и .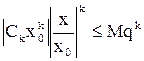

Сравнивая с помощью первого признака сравнения ряд (10.18) и сходящуюся геометрическую прогрессию

,

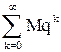получаем, что (4) сходится.

в) Этот пункт доказывается от противного.

Допустим, что найдется 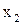такое, что 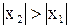для которого ряд (3) сходится. Тогда согласно пункту а) поскольку 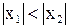он должен сходится в точке 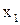. Противоречие.

Определение. Наибольшее значение 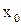такое, что в интервале 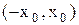степенной ряд (10.17) сходится, называется радиусом сходимости этого ряда (обозначается через 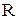), а интервал 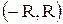называется его интервалом сходимости.

Из теоремы Абеля следует, что в интервале 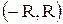ряд (3) сходится, а в интервалах 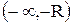и 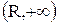он расходится (см. рис.2).

сходится

расходится расходится

Рис.2.

Сходимость ряда в точке 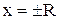исследуется дополнительно.

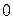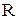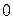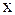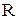Если ряд сходится только в точке , то считается равным , а если он сходится для всех , то считается равным .

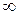Для определения радиуса сходимости 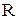имеются следующие формулы, получаемые из признаков Даламбера и Коши.

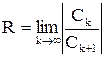, (5)

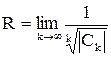(6)

Однако проще находить интервал сходимости путем непосредственного применения признаков Даламбера или Коши к абсолютным величинам членов ряда (5).

Пример22. Найдем область сходимости ряда .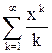

Исследуем абсолютную сходимость этого ряда с помощью признака Даламбера, получим

.

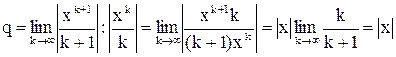Отсюда получаем, что при 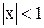, т.е. в интервале (-1,1) этот ряд сходится, а при 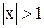, т.е. в интервалах 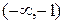и 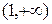он расходится. Поэтому радиус сходимости ряда 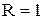и интервал сходимости есть (-1,1).

Исследуем концы этого интервала. Подставив 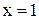в ряд, получим числовой ряд

,

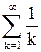который является гармоническим расходящимся рядом. Подставив 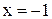, получим знакочередующийся ряд

.

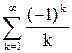Выше с помощью признака Лейбница было проверено, что он сходится. Окончательно получаем, что область сходимости исследуемого ряда есть

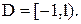
Дата добавления: 2014-01-06