Определения. Общее, частное, особые решения

Экономическая задача, приводящая к дифференциальному уравнению

Вопросы

Линейные дифференциальные уравнения. Уравнение Бернулли.

Обыкновенные дифференциальные уравнения

Лекция 3-4

Общее и частные решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения.

Уравнений в полных дифференциалах.

1. Определение обыкновенных дифференциальных уравнений.

2. Дифференциальные уравнения первого порядка.

3. Общее решение дифференциального уравнения.

4. Задачи Коши. Частное решение.

5.Определение дифференциального уравнения 1-ого порядка.

6. Дифференциальные уравнения с разделяющимися переменными.

7. Однородные дифференциальные уравнения.

8. Линейные дифференциальные уравнения первого порядка.

9.Уравнение Бернулли.

10.Уравнение в полных дифференциалах

Различные вопросы экономики приводят к необходимости решения уравнений, содержащей в качестве неизвестной некоторую функцию и ее производные до определенного порядка n.

Обозначим - величина фондов в натуральном или стоимостном выражении. Фонды – это станки, помещения и т.п. они изнашиваются, стареют, как говорят, выбывают. Скорость выбытия фондов – это производная , она выражается через коэффициент выбытия 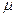. Например, если за 10 лет фонды полностью обновляются, то коэффициент выбытия равен 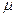=1/10. С другой стороны, инвестиции – вложение денег – ведут к увеличению фондов с коэффициентом пропорциональности 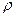. Учитывая все это, получим дифференциальное уравнение, вида:

.

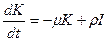Определения:

1. Уравнение, связывающее искомую функцию, её производные или дифференциалы, и аргументы, называется дифференциальным.
2. Наивысший порядок производной или дифференциала в записи уравнения называется порядком этого уравнения.
3. Решением дифференциального уравнения называется любая функция, если она и её производные или дифференциалы, будучи подставлены в уравнение, превращают его в тождество.
4. Дифференциальные уравнения относительно функции одной переменной (нескольких переменных) называются обыкновенными (в частных производных).

Пример 1.

а) 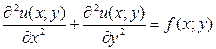- уравнение в частных производных второго порядка;

б) 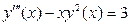- обыкновенное дифференциальное уравнение третьего порядка;

в) - обыкновенное дифференциальное уравнение первого порядка.

З а м е ч а н и е 1. В дальнейшем под словом уравнение будем понимать только обыкновенное дифференциальное уравнение.

Пример 2. Найти решения уравнений

а)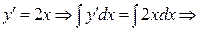

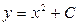(1)

Решение (1) уравнения первого порядка зависит от одной произвольной постоянной С, т.е. при различных значениях С получим разные решения. Теперь, для определения С, зададим одно дополнительное условие (начальные данные):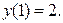

Отсюда из (1)следует: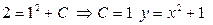

б)

(2)

Решение (2) уравнения 2- го порядка зависит от двух произвольных постоянных С₁ и С₂ необходимо задать уже два условия: . Отсюда

.

Геометрически решения (1) и (2) – семейство парабол. Задание начальных данных означает: из семейства парабол найти такую, которая в случае:

а) проходит через т.

б) проходит через т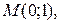таким образом, чтобы угловой коэффициент касательной в т. 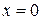равнялся .

Дата добавления: 2014-01-06