
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вид и общая структура решения
|
|
|
|
Рассмотрим неоднородное линейное уравнение  - го порядка
- го порядка
 (1)
(1)
где 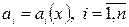 - коэффициенты уравнения (1), а
- коэффициенты уравнения (1), а 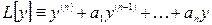 - линейный оператор. Очевидно, что
- линейный оператор. Очевидно, что 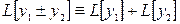 и
и  ,
, 
Теорема 1 (Пикара). Во всех точках некоторой области  , где
, где 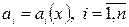 и
и  непрерывны, существует единственное решение задачи Коши для уравнения (1).
непрерывны, существует единственное решение задачи Коши для уравнения (1).
В дальнейшем полагаем, что 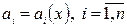 и
и  непрерывны в
непрерывны в  .
.
1. Общее решение линейного однородного уравнения.
 (2)
(2)
Определение 1. Функции 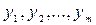 называются линейно независимости
называются линейно независимости 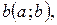 если существуют такие постоянные
если существуют такие постоянные  не все равные нулю, что
не все равные нулю, что

иначе – линейно зависимые.
Пример 1.
а) Функции 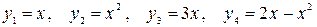 - линейно зависимые в
- линейно зависимые в 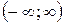 , так как при
, так как при
1) 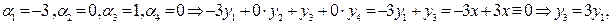
2) 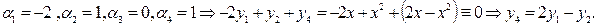
б) Функции  - линейно независимые в
- линейно независимые в 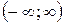 , так как
, так как  равно нулю только для двух значений
равно нулю только для двух значений 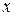 , а не для всех
, а не для всех 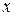 .
.
Линейная зависимость функции 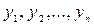 имеют непрерывные производные до
имеют непрерывные производные до 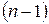 - го порядка включительно. Тогда определитель
- го порядка включительно. Тогда определитель
 называется определителем Воронского.
называется определителем Воронского.
Теорема 2. Если функции 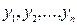 линейно зависимые в
линейно зависимые в  то
то 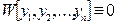
 .
.
Теорема 3. Если частные решения 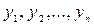 уравнения (2) линейно независимые в
уравнения (2) линейно независимые в 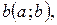 то
то 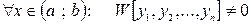 .
.
Определение 2. Любая система из  линейно независимых частных решений уравнения (2) называется фундаментальной системой.
линейно независимых частных решений уравнения (2) называется фундаментальной системой.
Теорема 4. Для уравнения (2) всегда существует фундаментальная система.
Теорема 5. Если 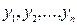 - частные решения уравнения (2), то
- частные решения уравнения (2), то
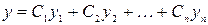 , (3)
, (3)
где 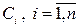 - произвольные постоянные, также будет решением уравнения (2).
- произвольные постоянные, также будет решением уравнения (2).
Решение (3) содержит  произвольных постоянных. При каких условиях (3) будет общим решением уравнения (2).
произвольных постоянных. При каких условиях (3) будет общим решением уравнения (2).
Теорема 6. Если частные решения 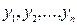 уравнения (2) образуют фундаментальную систему, то (3) является общим решением уравнения (2).
уравнения (2) образуют фундаментальную систему, то (3) является общим решением уравнения (2).
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 361; Нарушение авторских прав?; Мы поможем в написании вашей работы!