Основные понятия о функциях нескольких переменных

Вопросы

Дифференцирование неявных функций

Дифференцирование функций нескольких переменных.

Предел и непрерывность функции многих переменных.

Функции многих переменных.

Лекция 1

1.Определение функции многих переменных и примеры таких функций в экономике.

2. Предел и непрерывность функции многих переменных.

3. Что называется частной производной функции многих переменных и их экономический смысл?

5. Какими правилами и формулами можно воспользоваться для вычисления частных производных?

6. Что называется дифференциалом функции многих переменных?

7. При каком условии значение смешанной производной не зависит от порядка дифференцирования.

8. Производные неявных функций, пример неявной функции из экономики.

До сих пор в курсе высшей математики мы рассматривали в основном действительные функции одной действительной переменной вида , т.е. функции, области определения и области значений которых являлись некоторыми подмножествами на числовых осях.

Однако на практике широко используются функции, имеющие более одного аргумента, исследование которых имеет свои особенности.

Например, ес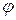ли и есть долгота и широта точки на поверхности Земли и – высота этой точки над уровнем моря, то поверхность Земли задает функцию двух переменных

,

определенную для всех допустимых значений 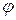,и принимающую действительные значения.

Если – координаты точки находящейся внутри некоторой детали и 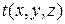– температура в этой точке детали, то закон распределения температуры внутри детали задается функцией трех переменных

,

область определения которой, определяется формой этой детали.

Определение. Функцией двух (трех) переменных называется функция, область определения которой есть некоторое подмножество на плоскости (в пространстве), а область значений 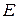принадлежит действительной оси.

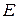Если принадлежит плоскости , а оси 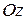, то такую функцию двух переменных записывают в виде

.

Если а 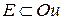, то эту функцию трех переменных можно записать в виде

.

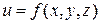Введем некоторые определения, относящиеся к областям на плоскости или в пространстве.

Определение. Окрестностью точки на плоскости (или в пространстве) радиуса называется круг без окружности (или шар без сферы) радиуса с центром в точке .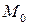

Такую окрестность будем обозначать .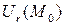

На плоскости 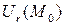определяется неравенством

а в пространстве – .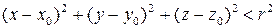

Определение. Точка 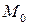называется граничной точкой для множества , если окрестность любого радиуса этой точки пересекается как с множеством , так и с его дополнением.

Множество всех граничных точек множества называется границей этого множества и обозначается .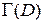

Определение. Множество , содержащее всю свою границу 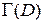, называется замкнутым. Множество , не содержащее ни одной точки своей границы, называется открытым.

Примеры.

1) Окрестность 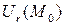не содержит ни одной точки своей границы – окружности (или сферы), поэтому 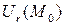– открытое множество.

2) Круг на плоскости задаваемый неравенством

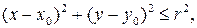
содержит свою границу – окружность

поэтому он – замкнутое множество.

3) Четверть плоскости определяется системой неравенств

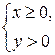
содержит часть своей границы, расположенной на оси и не содержит часть границы на оси Это множество не является ни открытым, ни замкнутым.

Пусть 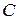– число. Линией уровня 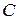функции называется множество всех точек 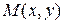из области определения , координаты которых удовлетворяют уравнению .

Таким способом изображаются, например, линии равной высоты на географических картах. Они являются линиями уровня функции определяющей высоту точки местности с координатами 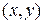над уровнем моря.

Например. Найдем линии различного уровня функции

.

Такие линии определяются уравнением

.

При , получим ; .

Поэтому линия уровня есть окружность радиуса 1 с центром в начале координат.

При 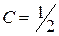, получим 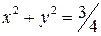. Линия уровня 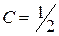есть окружность радиуса с центром в начале координат. При 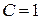, уравнение определяет точку начало координат (см. рис.1).

Рис.1.

Определение. Поверхностью уровня 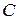функции 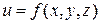называется множество всех точек 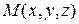из области определения функции, координаты которых удовлетворяют уравнению

Пример. Рассмотрим функцию . При 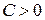, ее поверхностями уровня являются сферы радиуса 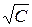с центрами в начале координат. При , поверхность уровня есть начало координат. Поверхности уровня 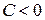у этой функции отсутствуют.

Дата добавления: 2014-01-06