Закон больших чисел

Из этой формулы вытекает вероятность заданного отклонения

.

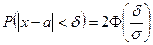Как известно, нельзя заранее уверенно предвидеть какое из возможных значений примет случайная величина в итоге испытания. Но оказывается, что при некоторых сравнительно широких условиях, суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным, т.е. можно предвидеть ход явления. Эти условия и указываются в теоремах, носящие общее название закона больших чисел.

Теорема Чебышева. При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию.

Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера.

Ответ на то, при каких условиях это правомерно, дает теорема Чебышева:

Рассмотрим результаты каждого измерения как случайные величины .

К этим величинам можно применить Теорему Чебышева, если:

1. Они попарно независимы - (результат каждого измерения не зависит от результатов остальных).

2. Имеют одно и тоже МО – (измерения проведены без систематических (одного знака) ошибок). В этом случае МО всех случайных величин одинаковы и равны истинному размеру .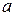

3. Дисперсии их равномерно ограничены (прибор обеспечивает определенную точность измерений (рассеивание ограничено)).

З а м е ч а н и е. Ошибочно думать, что увеличивая число измерений, можно достичь сколь угодно большой точности. Это ограничивается тем, что сам прибор дает показания с точностью .

На Теореме Чебышева основан широко применяемый в статистике выборочный метод,, суть которого в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон наудачу отобранных из различных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое число волокон.

Или определение качества зерна по небольшой его пробе. Число наудачу отобранных зерен мало по сравнению со всей массой зерна, но само по себе оно достаточно важно.

Теорема Бернулли. При неограниченном увеличении числа независимых испытаний в постоянных условиях частота рассматриваемого события 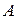сходится по вероятности к его вероятности в отдельном опыте, т.е.

.

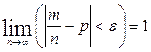Примеры из экономики. Закон больших чисел утверждает, что при очень большом числе случайных явлений средний их результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Пример 1. Хотя невозможно предсказать, какую конкретную сумму снимет или положит на свой счет очередной клиент банка, суммарное значение этих операций за день остается примерно одним и тем же в обычные будничные дни.

Пример 2. Крупный банк ведет множество финансовых операций: на межбанковском рынке кредитует другие банки, продает и покупает акции и облигации и т.п. При этом проигрыш по некоторым направлениям компенсируется выигрышем на других, что обеспечивает банку устойчивое финансовое положение.

Эта стратегия работы банка соответствует народной мудрости: «не клади все яйца в одну корзину» - и представляет разумный принцип работы на финансовом рынке. Научное название этого принципа принцип диверсификации, он означает, что нужно проводить разнообразные, не связанные друг с другом операции, тогда убытки от одних операций будут покрыты прибылью от других операций. Диверсификация ведет к усреднению дохода и уменьшению риска.

Литература

1. Гнеденко Б.В. Курс теории вероятности. М.: Высшая школа, 1969г.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998г.

3. Чистяков В.П. Курс теории вероятностей. М.: Высшая школа, 1982г.

4. Вентцель Е.С., Овчаров Л.А. Теория вероятностей (задачи и упражнения). М.:

Высшая школа, 1973г.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математи

ческой статистики. М.: Высшая школа, 1998г.

7. Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики

(типовые расчета). М.: Высшая школа, 1983 г.

Дата добавления: 2014-01-06