Предел и непрерывность функции нескольких переменных

Рассмотренные выше понятия функций двух или трех переменных можно обобщать на случай переменных.

Определение. Функцией переменных 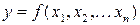называется функция, область определения которой принадлежит , а область значений – действительной оси.

Такая функция каждому набору переменных из сопоставляет единственное число .

В дальнейшем для определенности мы будем рассматривать функции 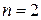переменных, но все утверждения сформулированные для таких функции остаются верными и для функций большего числа переменных.

Определение. Число называется пределом функции

в точке , если для каждого найдется такое число что при всех 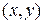из окрестности , кроме этой точки, выполняется неравенство

.

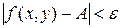Если предел функции в точке равен , то это обозначается в виде

.

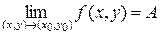Практически все свойства пределов рассмотренные нами ранее для функций одной переменной остаются справедливыми и для пределов функций нескольких переменных, однако практическим нахождением таких пределов мы заниматься не будем.

Определение. Функция называется непрерывной в точке если выполняется три условия:

1) существует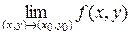

2) существует значение функции в точке

3) эти два числа равны между собой, т.е. .

Практически исследовать непрерывность функции можно с помощью следующей теоремы.

Теорема. Любая элементарная функция непрерывна во всех внутренних (т.е. не граничных) точках своей области определения.

Пример. Найдем все точки, в которых функция

непрерывна.

Как было отмечено выше, эта функция определена в замкнутом круге

.

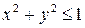Внутренние точки этого круга является искомыми точками непрерывности функции, т.е. функция непрерывна в открытом круге .

Определение понятия непрерывности в граничных точках области определения функции возможно, но мы этот вопрос в курсе затрачивать не будем.

Дата добавления: 2014-01-06