Закон равномерного распределения вероятностей

Материал основной части лекции

ПЛАН

Владимир 2012

Л Е К Ц И Я

по дисциплине «Теория вероятностей и математическая статистика» для бакалавров направления 080100.62 «Экономика»

Тема № 2. Случайные величины и их законы распределения.

Занятие № 2.10 Основные законы распределения вероятностей случайных величин.

Вид занятия: лекция (12)

Литература: 1). Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб.пособие для вузов.-8-е изд.,стер.-М.:Высш.шк.,2002-479 с. (122-123,149-151,146). 2.) Вентцель Е.С. Теория вероятностей. Учебник М.: Гос.издат.физ.мат.лит-ры., 1958-464с.(99-101,309-310).

проведения занятия

№ п/п	Учебные вопросы занятия	Время, мин.
I. II	Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть.	2-3
	1. Закон равномерного распределения вероятностей. 2. Показательный закон распределения. 3. Распределение Стьюдента.
	Заключительная часть	2-3
	Подведение итогов занятия. Выдача задания на самостоятельную работу.

При решении задач, которые выдвигает практи­ка, приходится сталкиваться с различными распределе­ниями непрерывных случайных величин. Плотности рас­пределений непрерывных случайных величин называют также законами распределений. Часто встречаются, на­пример, законы равномерного, нормального и показатель­ного распределений. В настоящем параграфе рассматри­вается закон равномерного распределения вероятностей. Нормальному и показательному законам посвящены сле­дующие две главы.

Распределение вероятностей называют равномерным , если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Приведем пример равномерно распределенной непре­рывной случайной величины.

Пример. Шкала измерительного прибора проградуирована в не­которых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, которая может принимать с постоянной плотностью вероятности лю­бое значение между двумя соседними целыми делениями. Таким об­разом, Χ имеет равномерное распределение.

Найдем плотность равномерного распределения f(x), считая, что все возможные значения случайной величины заключены в интерва­ле (а, b ), на котором функция f(x) сохраняет постоянные значения:

По условию, Χ не принимает значений вне интервала (а, б ), поэтому f(x)=0 при x < α и x > b.

Найдем постоянную С. Так как все возможные значения слу­чайной величины принадлежат интервалу (а, b ), то должно выпол­няться соотношение

Отсюда

Итак, искомая плотность вероятности равномерного распределе­ния

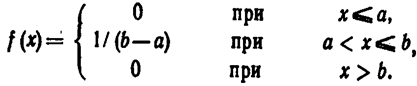
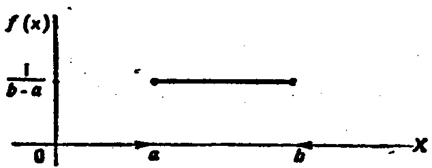
График плотности равномер­ного распределения изображен на рис. 1, а график функции распре­деления—на рис. 2.

Замечание. Обозначим че­рез R непрерывную случайную ве­личину, распределенную равномер­но в интервале (0, 1), а через r — ее возможные значения. Ве­роятность попадания величины R (в результате испытания) в интервал (с, d), принадлежащий интер­валу (0, 1), равна его длине:

Действительно, плотность рассматриваемого равномерного рас­пределения

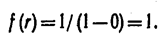
Следовательно, вероятность попадания случайной величины R в ин­тервал (с, d) (см. Лекцию 2.8)

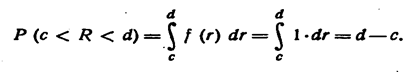
Далее случайная величина R используется неоднократно.

Дата добавления: 2014-01-07