Загальний характер руху і деформації рідких часток

У цілому картина руху рідини визначається поведінкою її окремих часток. Тому їх дослідження є важливим для вивчення руху рідини. З цієї точки зору істотне значення для розуміння кінематики є теорема Коші-Гельмгольца, суть якої формулюється так: усякий рух елементарного об’єму рідини у дану мить часу можна розкласти на три простих рухи: 1) поступальний, разом з довільно вибраним полюсом; 2) обертальний довкола миттєвої осі, яка проходить через вибраний полюс; 3) рух, зумовлений деформацією.

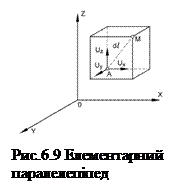Для доведення сформульованої теореми виберемо у потоці нев’язкої рідини довільну точку А з координатами x, y, z. Нехай за час dt вибрана нами частка рідини переміститься в положення М на відстані dl від точки А. На відрізку dl траєкторії частки, як на діагоналі, побудуємо елементарний паралелепіпед з ребрами dx, dy, dz, паралельними координатним осям (рис.6.9).

Позначимо початкову швидкість в точці А через , а її компоненти через u_x=f₁(x,y,z), u_y=f₂(x,y,z), u_z=f₃(x,y,z). тоді компоненти швидкості у точці М будуть

u_x(M)=f₁(x+dx; y+dy; z+dz);

u_y(M)=f₂(x+dx; y+dy; z+dz); (6.19)

u_z(M)=f₃(x+dx; y+dy; z+dz)

Розкладемо вирази (6.19) у ряд Тейлора, відкидаючи нескінченно малі порядки вище першого. В результаті отримаємо такі вирази для компонентів швидкості в точці М:

;

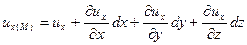; (6.20)

.

Таким чином, різні точки паралелепіпеда матимуть різні швидкості, тому паралелепіпед буде деформуватися.

Перетворимо першу формулу системи (6.20), додавши і віднявши вираз

Тоді перше рівняння системи (6.20) можна переписати так:

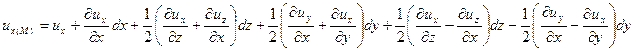
Після аналогічних перетворень дві інші формули набудуть вигляду

Для того, щоб спростити формули для компонентів швидкості у т. М і надати їм бажаної структури, введемо такі позначення (див.6.12-6.17):

Тоді компоненти швидкості в т. М можна записати у вигляді

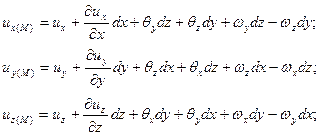(6.21)

Розглянемо фізичний зміст доданків у цих рівняннях.

Часткові диференціали 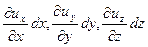виражають швидкості деформації абсолютного видовження або стиску вздовж координатних осей.

Що стосується величин q_x, q_y, q_z, то вони враховують інтенсивність деформації і характеризують кутову швидкість зсуву.

Величини ω_x, ω_y, ω_z, виражають ступінь обертання рідини і становлять компоненти так званої вихрової швидкості.

Дійсно, коли б частка була твердою і оберталася довкола миттєвої осі з кутовою швидкістю ω, то, як показано вище, проекції вектора кутової швидкості становили б (6.15-6.17)

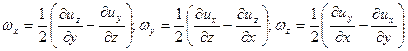
Вектор , проекції якого W _x=2ω_x, W _y=2ω_y, W _z=2ω_z, називається вихором швидкості або просто вихором.

Таким чином, відповідно до отриманої системи рівнянь (6.21) рух рідкої частки можна представити як геометричну суму трьох швидкостей: поступальної швидкості полюса з компонентами поступальної швидкості u_x, u_y, u_z, швидкості деформації з компонентами лінійної деформації 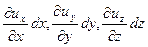і компонентами деформації зсуву q_ydz+q_zdy, q_zdx+q_xdz, q_xdy+q_ydx, а також швидкості обертального руху з компонентами ω_ydz-ω_zdy, ω_zdx-ω_xdz,ω_xdy-ω_ydx. Цей висновок є змістом теореми Коші-Гельмгольца, тобто

(6.22)

Дата добавления: 2014-01-07