Приклад 1.2

Властивості оцінок

План

Тема: Оцінки

Лекція № 16

Приклад 1.1.

Наведемо результати моделювання за допомогою пакету MATHCAD (для такої нескладної задачі може бути використаний будь-який інший математичний або статистичний пакет програм і навіть EXCEL з використанням пакету “аналіз даних”) Вихідні дані знаходяться в табл.1 (E(a) у таблиці означає показниковий (експоненційний) розподіл з математичним сподіванням, рівним a, α=sup |F_n(x)-F(x)| ).

Таблиця 1

¹	Закон	n	a	¹	Закон	n	a
	R [0, 2]		0.03		N (1,4)		0.01
	N (2, 0.25)		0.02		E (5)		0.03
	E (3)		0.01		R [0.3]		0.1
	R [1, 3]		0.02		N (1,4)		0.3
	N (1, 1)		0.01		E (1)		0.2
	E (2)		0.03		R [1,3]		0.03
	R [2, 3]		0.01		N (1,1)		0.02
	N (0, 4)		0.03		E (2)		0.01
	E (3)		0.02		R [2,3]		0.02
	R [0, 2]		0.03		N (2,1)		0.01
	N [2, 1]		0.02		E (3)		0.03
	E (4)		0.01		R [1,2]		0.01
	R [1, 2]		0.02

1. Властивості оцінок

2. Теоретичне порівняння оцінок

3. Статистичне порівняння оцінок

Нехай x₁,..., x_n — вибірка, тобто n незалежних випробувань випадкової величини X, що має функцію розподілу F(x / a), яка залежить від параметра a, значення якого невідомо. Потрібно оцінити значення параметра a.

Оцінкою â = j(x₁,..., x_n) називається функція спостережень, яка використовується для наближеного визначення невідомого параметра. Значення â оцінки є випадковою величиною, оскільки (x₁,..., x_n) — випадкова величина (багатовимірна).

1. Оцінка â = j(x₁,..., x_n) називається спроможною, якщо при n ® ¥ â ® a за імовірністю при будь-якому значенні a.

2. Оцінка â = j(x₁,..., x_n) називається незсуненою, якщо при будь-якому a такому, що Mâ = M j(x₁,..., x_n) = a.

Спроможність є обов'язковою властивістю оцінок, що використовуються. Властивість незсуненості є бажаною; багато з оцінок, які використовуються на практиці цієї властивості не мають.

3. Оцінка j* називається оптимальною, якщо для неї середній квадрат помилки

M(â- a)²= M [ j*(x₁,..., x_n) - a ] ²= min M [ j(x₁,..., x_n) - a ] ²

мінімальний серед всіх оцінок {j}; тут критерієм якості оцінки прийнятий квадрат помилки (â - a) ². У більш загальній ситуації, якщо критерієм якості покладено деяку величину L(â, a), що носить назву функції втрат (чи функції штрафу), то оптимальною оцінкою є та, для якої величина ML(â, a) є мінімальною, де останній вираз є функцією невідомого a і називається функцією умовного ризику. Ясно, що оптимальної оцінки може не існувати (тому що характеристикою є функція, а не число).

Нехай на заводі є велика партія з N (тисячі) транзисторів, які використовуються для складання деякого приладу. Вихідні параметри приладу (наприклад, надійність, рівень шуму, імовірність виходу з режиму і т.д.) залежать від зворотніх струмів транзисторів; зворотній струм у різних екземплярів різний, і тому можна вважати його випадковою величиною, при цьому, як відомо технологам, розподіленою рівномірно в діапазоні від 0 до I _max, де I _max - поріг відбраковування, який встановлено на заводі - виготовлювачі транзисторів. Отже, вихідні параметри приладу визначаються величиною I _max. Припустимо, що за якимись причинами значення I _max виробнику приладів невідомо. Ясно, що в цьому випадку з партії потрібно випадковим чином витягти n (порівняно небагато: десятки) транзисторів, вимірити їхній струм, і по вимірах оцінити I _max (невідомий параметр а). Таким чином, виникає статистична задача: за спостереженнями x₁,..., x_n над випадковою величиною C, розподіленої рівномірно на відрізку [0, a ], оцінити невідомий параметр a.

Порівняємо три способи оцінювання (три оцінки): оцінку, отриману методом моментів,

â₁ = , (2.1)

оцінку, отриману методом максимальної правдоподібності (після виправлення зсуненості),

â₂ = 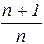max x_i (2.2)

і оцінку, отриману методом порядкових статистик,

â ₃ = 2 _0.5 = x_(k) + x_(k+1), (2.3)

де _0.5 =— вибіркова квантіль порядку 0.5, тобто вибіркова медіана; x_{(k )} — член варіаційного ряду з номером k; тут зроблено припущення n = 2k. Точність цих оцінок можна порівняти теоретично й експериментально (статистично).

Зауваження. Точність, однак, не є єдиним критерієм якості оцінок. Дуже важливо, наприклад, властивість стійкості оцінки до зміни закону розподілу до засмічення; у цьому змісті, як виявляється, â ₃ — найбільш гарна, а â ₂ — найменш; дійсно, нехай, наприклад, у нашу вибірку випадково потрапило спостереження, що різко перевершує всі інші (у випадку з партією тріодів, якщо потрапив тріод, що не пройшов відбраковування); значення оцінки â ₂ різко зміниться, значення â ₃ майже не зміниться.

Дата добавления: 2014-01-07