Описання похибок за допомогою моментів

Описання похибок за допомогою функцій розподілу є універсальним, проте досить трудомістким. Тому використовуються і інші форми описання. Наприклад, за допомогою обмеженого числа величин, що звуться моментами.

Початковий момент:

. (5.18)

Із (5.18) слідує:

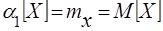(5.19)

(5.19) – перший початковий момент.

Центральний момент:

(5.20)

Перший центральний момент:

(5.21)

Як для похибки, так і для результату можна побудувати систему моментів.

Другий центральний момент називають дисперсією розподілу результатів спостережень, та позначають D[Х]:

D[X] = D[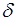] = M[(X - m_x)²] = M[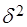] = =. (5.22)

Дисперсіяхарактеризує розсіюваннярезультатувідносно математичного чекання. По аналогії з інтерпретацією математичного чекання, дисперсія аналогічна моменту інерції центра ваги фігури, що обмежена функцією розподілу та віссю абсцис.

Але, так як розмірність дисперсії – квадрат вимірюваної величини, то на практиці частіше використовують середнє квадратичне відхилення:

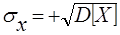. (5.23)

З його допомогою можна оцінити вірогідність того, що при однократному спостереженні випадкова похибка по абсолютній величині не перевищить деяку наперед задану величину :

Р; (5.24)

(5.24) - нерівність Чебишева.

Для описання розподілу результатів використовуються і моменти більш високих порядків. Так, третій момент описує асиметрію функції розподілу, а четвертий служить для характеристики гостро- або плосковершинності функції.

Дата добавления: 2014-01-07