Деякі особливості обчислення середніх величин

Досить часто у плануванні та економічному аналізі осереднюваний показник – не абсолютна, а відносна величина. Наприклад, обчислення середнього процента виконання дерзамовлення за відомими процентами виконання дерзамовлення двома міністерствами.

Вибір форми середньої залежить від наявної інформації.

Слід пам”ятати, що у середньої, яка визначається з відносних величин, вагами не є частоти, а знаменники тих співвідношень, що обчислюють індивідуальні відносні величини.

Якщо в розпорядженні є безпосередні дані, що характеризують знаменник, то форма середньої – середня арифметична зважена.

Якщо такі дані відсутні, то знаменник потребує додаткових обчислень, а форма середньої, яку необхідно буде застосувати – середня гармонійна.

Приклад. Визначити середню частку тканин з індексом “Н” по двох видах тканин у цілому (табл.9.1).

Таблиця 9.1

Вихідні дані для обчислення середньої частки

Тканини	Загальний обсяг виробництва, млн. п.м	Частка тканин з індексом “Н”,%
Бавовняні	591,6	25,0
Шовкові	221,4	19,3
Разом	813,0	х

Тут варіантами є частки цих тканин по окремих їх видах. Із них неможливо знайти середню арифметичну просту тому, що обсяг їх виробництва різний.

Частка “Н”,%= .

Чисельник відсутній. Необхідно визначити обсяги бавоввняних і шовкових тканин з індексом “Н”.

Тоді у формалізованому вигляді середня частка тканин з індексом “Н” буде дорівнювати

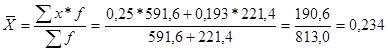або 23,4%.

Приклад. Визначити середню частку забракованої продукції за всіма видами харчів у цілому (табл.9.2).

Таблиця 9.2

Вихідні дані для визначення середньої частки забраковоної продукції

Види харчів	Забраковано, т	Частка забракованої продукції у загальному обсязі перевіреної,%
М”ясо	473,1	6,1
Ковбасні вироби	107,3	11,1
Копченості	153,4	13,5
Разом	733,8	х

Частка забракованої продуцікї = .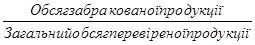

Знаменник цієї логічної формули відсутній. Його необхідно визначити додатково. Якщо знаменник невідомий, значить частка буде розраховуватися за середньою гармонійною.

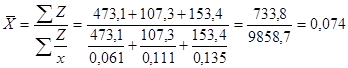або 7,4%.

Свої особливості мають розрахунки середніх для ознак порядкової та номінальної шкал, тобто ознак, які не можуть бути виміряні. Якщо ранги порядкової шкали відображають приблизно однакові відстані між окремими якостями явищ, середній ранг обчислюють як і для ознак метричної шкали.

В окремих випадках може бути, що ранги – числа додатні і від”ємні (наприклад, оцінка ступеня задоволеності професією), то середні ранги по кожній групі будуть обчислені за середньою арифметичною зваженою та можуть бути як додатніми, так і від”ємними.

Приклад. Якщо ранги мають і додатні, і від”ємні значення (табл.9.3).

Таблиця 9.3

Дані для розрахунку ступеня задоволеності професією

Ступінь задоволе-ності	Бал,	Чисельність робітників	Розрахунок величини
оператори,	налагоджу-вальники,
Задоволені
Байдужі
Незадоволені	-1			-30	-34
Разом	х			-12

Середній ранг по кожній професії:

;

.

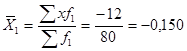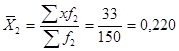Нормований середній бал (змінюється від –1 до +1) задоволеності буде від”ємним у опереторів і додатнім у налагоджувальників.

Приклад. Якщо ранги мають тильки додатні значення, то визначається нормований середній бал за формулою

,

де - середньозважений ранг (),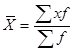

- ранг ознаки;

R – розмах шкали рангів; ;

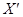- середня шкала рангів; .

Для альтернативної ознаки (приймає значення взаємовиключні 1 або 0) середня – це частка елементів сукупності з ознакою, що цікавитьдослідника.

.

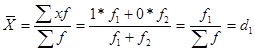Приклад. Із 230 робітників 46 мають намір змінити професію. Визначити середній рівень професійної мобільності робітників.

Він буде дорівнювати

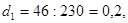тобто 20%.

Інколи виникає потреба у визначенні багатомірної середньої – узагальнюючого показника міри двох і більше ознак, які мають різні одиниці виміру. Її розрахунок базується не на індивідуальних значеннях ознак , а на їх відношеннях до середньої по сукупності в цілому, тобто

; .

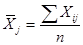Формула багатомірної середньої має такий вигляд:

,

де m – число ознак.

Ця середня характеризує місце j-елемента в багатомірному просторіє

Приклад. Визначити багатомірну середню для характеристики розвитку охорони здоров”я (табл. 9.4).

Таблиця 9.4

Вихідні дані по областях України, де необхідно виявити рівень охорони здоров”я.

Область	У розрахунку на 10000 тис. осіб населення	Співвідношення
Лікарів	сер. мед.перс.	лікарн. ліжка
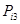
Дніпропетровська	44,3	115,0	139,5	1,009	0,993	1,036	1,013
Донецька	43,9	125,1	139,0	1,000	1,080	1,032	1,037
Запорізька	43,5	109,1	138,8	0,991	0,942	1,030	0,988
Харківська	48,8	109,3	131,9	1,112	0,944	0,979	1,012
Україна	43,9	115,8	134,7	1,000	1,000	1,000	1,000

; ; .

Базою зіставлення є останній рядок (середній рівень країни). Середня із відносних величин для Дніпропетровської області

.

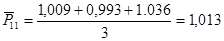Дата добавления: 2014-01-07