Порядкові середні

До порядкових середніх належать мода та медіана. Це, так як і середня арифметична, - характеристики центру розподілу. Їх розглядають разом із такими характеристиками розподілу як квантилі та децилі.

Мода () – це та варіанта, що найчастіше повторюється в ряді розподілу.

Для дискретного ряду – це варіанта, якій відповідає найбільша частота (легко шукати візуально).

Для інтервального ряду – візуально легко шукати модальний інтервал (інтервал, що має найбільшу частоту), а сама мода визначається за формулою

,

де - нижня межа модального інтервалу;

- ширина модального інтервалу;

- частоти перед-, модального та післямодального інтервалів.

Медіана () – це варіанта, що ділить ранжирований ряд на дві рівні за чисельністю частини.

Якщо в ряді непарне число варіант, записаних у порядку зростання чи зменшення, то медіаною буде центральна варіанта.

Якщо в ряді парне число варіант, то медіаною буде середня арифметична двох центральних варіант.

При визначенні медіани в рядах розподілу використовують кумулятивні частоти (накопичені частоти), які полегшують пошук центральної варіанти.

Для дискретного ряду – встановлюють номер центральної варіанти, ділячи загальну кількість елементів на два. Медіана – це варіанта, номер якої знаходиться в групі, що містить номер центральної ознаки в рядку кумулятивних (накопичених) частот.

Для інтервальних рядів спочатку визначається медіанний інтервал, для якого кумулятивна (накопичена) сума частот рівна або перевищує половину загального обсягу елементів сукупності. Сама медіана визначається за формулою

,

де - нижня межа медіанного інтервалу;

- ширина медіанного інтервалу;

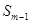-кумулятивна (накопичена) частота передмедіанного інтервалу;

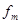- частота медіанного інтервалу.

Якщо медіана ділить варіаційний ряд на дві однакові за обсягом частини, то в кожній частині, в свою чергу, можна знайти варіанту, яка поділить її на підгрупи. Таки варіанти називають квартилями Q. 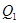- перший квартиль – відсікає четверть сукупності знизу; - третій квартиль – відсікає четверть сукупності зверху; 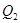- другий квартиль – це медіана.

На відміну від середньої арифметичної, яка є абстрактною величиною, мода та медіана завжди збігаються з конкретними варіантами, на них не впливають значення нехарактерних для сукупності варіант, при їх обчисленні до уваги не потрібно брати всі без виключення варіанти (як при визначенні середньої арифметичної).

Дата добавления: 2014-01-07