Блочно-ієрархічний підхід до моделювання складних систем

Цей підхід містить у собі синтез і аналіз технічних об'єктів.

Аналіз технічних об'єктів – це вивчення властивостей останніх. Цей підхід не ставить завдання створення нових об'єктів, а досліджує тільки дані.

Синтез технічних об'єктів – це створення нових варіантів об'єктів. Для дискретних об'єктів синтез – це завдання визначення структури. Для безперервних об'єктів завдання синтезу – це завдання визначення їх структури і чисельних величин внутрішніх параметрів. У багатьох випадках ці завдання необхідно розрізняти, що і відбилося в термінології «синтез структури» і «розрахунок внутрішніх параметрів» (структурний синтез, параметричний синтез). Виникають завдання структурної і параметричної оптимізації (системна оптимізація).

Параметрична оптимізація припускає, що зв'язок об'єкта керування зі зовнішнім стосовно об'єкта середовищем не змінюється і завдання полягає у відшуканні вектора керованих параметрів:

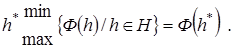(2.1)

Кожній точці простору керованих параметрів відповідає певна сукупність значень параметрів h_k, k Є К, що встановлює значення вектора h =∑ h_k, k Є К. Цю точку (безліч точок h), що відповідає конкретному етапу проектування, будемо називати точкою, що відображає. Наведена постановка задачі параметричної оптимізації справедлива не тільки при розгляді внутрішніх параметрів об'єкта, але і вихідних параметрів. Оптимізація останніх зв'язана з послідовним переходом (відповідно до заданого алгоритму) із простору внутрішніх у простір вихідних параметрів. Наприклад, нехай є цільова функція F(x,h), де h – вектор внутрішніх, а х – вектор вихідних параметрів. Задано безліч векторних обмежень Х Є х і завдання полягає у відшуканні вектора

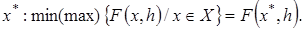(2.2)

У цій постановці вектор внутрішніх параметрів характеризується як деяка інтегральна константа, а це значить, що ми маємо традиційну задачу математичного програмування. Застосування схеми параметричної декомпозиції приводить до задачі (2.1), що може бути визначена шляхом послідовного розв’язання задач вигляду (2.2) для різної сукупності компонентів вектора внутрішніх параметрів.

Структурна оптимізація припускає, що зв'язок об'єкта керування з зовнішнім середовищем змінюються. Донедавна механізм структурної оптимізації припускав тільки прямий перебір різних варіантів. З формальної точи зору це пояснювалось відсутністю інформації про властивості критеріальних функцій (безперервність, дифференціальність) і, як наслідок, неможливість вибору напрямку оптимізації. Такий підхід не тільки малоефективний, але в багатьох випадках і просто збитковий. У даний час розв’язання задач структурної оптимізації на основі імітаційного моделювання дозволило зробити якісний стрибок у цьому напрямку. Так, зокрема, одержання відповідної інформації про властивості об'єкта в заданій точці, що відображає (чи її досить малому оточенні) на основі імітаційного моделювання, є ефективним шляхом розв’язання широкого класу завдань аналізу об'єкта.

Задачі аналізу класифікують у такий спосіб. За частотою застосування їх поділяють на типові й нетипові. Типові задачі широко використовують при проектуванні найрізноманітніших об'єктів. Нетипові задачі зв'язані з необхідністю одержання деякої додаткової інформації і вимагають розробки спеціальних алгоритмів.

За іншою ознакою їх класифікують на задачі одноваріантного і багатоваріантного аналізу.

Розв’язання задач одноваріантного аналізу подає інформацію про вихідні параметри об'єкта безпосередньо в заданій точці, що відображає. Формально це пов'язано з однократним вирішенням системи рівнянь чи однократним випробуванням макета об'єкта.

Типові задачі одноваріантного аналізу:

1) аналіз статистичного стану;

2) аналіз перехідного процесу;

3) аналіз частотних характеристик;

4) аналіз стійкості;

5) аналіз стаціонарних режимів коливань.

Багатоваріантний аналіз – багаторазове здійснення одноваріантного аналізу – зв'язаний з дослідженням поводження об'єкта в деякому оточенні точки, що відображає. Типові задачі багатоваріантного аналізу:

1) статистичний аналіз;

2) аналіз чутливості.

Одноваріантний аналіз дає відповідь на запитання, чи виконуються умови, необхідні для функціонування об'єкта заданої структури при номінальних значеннях внутрішніх параметрів. Статистичний же аналіз відповідає на запитання, з якою імовірністю будуть виконуватися ці умови працездатності. Ця імовірність характеризує такі властивості проектованого об'єкта, як надійність і серійна здатність.

Аналіз чутливості дозволяє визначити ступінь впливу внутрішніх і зовнішніх параметрів на вихідні параметри. Цей аналіз необхідний при оцінці нестабільності вихідних параметрів в умовах впливу зовнішніх дестабілізуючих факторів. Крім того, він дозволяє одержати інформацію про те, в якому напрямку і які керовані параметри варто застосовувати в процесі оптимізації.

Структура і принцип побудови математичних моделей світлотехнічних і електротехнічних розрахунків

Дата добавления: 2014-01-07